Le blog de Balise

Introduction à la complexité algorithmique – 2/2

Publié le 11 février 20139 novembre 2013 par Balise8 commentaires

Dans l’épisode précédent, j’ai expliqué deux manières de trier des livres et j’ai tenté de justifier combien de temps, en nombre d’opérations élémentaires, ça me prenait de faire ça, et j’ai évalué le nombre maximum d’opérations en fonction du nombre de livres que j’avais à trier.

Je suis arrivée aux conclusions suivantes :

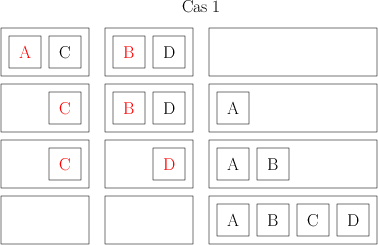
pour le « premier » tri, celui où je regarde à chaque étape où je dois mettre le livre suivant en parcourant tous les livres que j’ai mis jusqu’ici, j’ai, dans le meilleur des cas, 2n – 1 opérations, dans le pire des cas (n² + n)/2 opérations, et dans le cas moyen (n²+9n)/4 opérations.
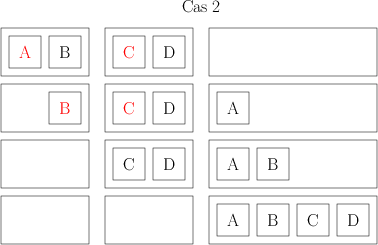
pour le « deuxième » tri, celui où je combine mes ensembles de livres deux par deux, j’ai, dans tous les cas, 2*n*log(n) opérations.

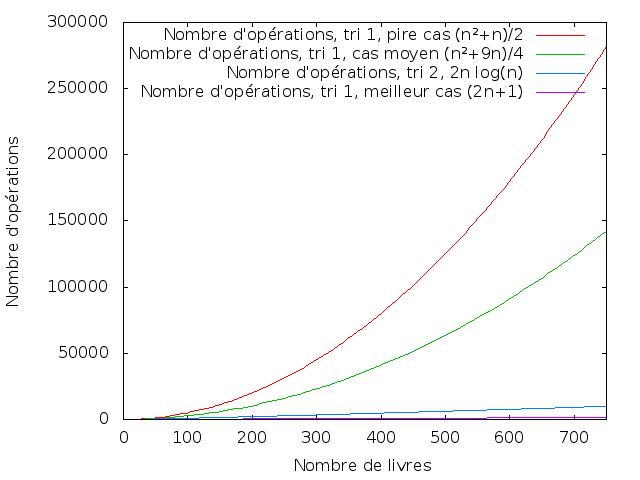
Je vais me permettre une petite courbe ici parce que les courbes c’est joli.

Au cas où j’aurais des daltoniens parmi mes lecteurs, les courbes sont, de haut en bas, dans l’ordre de la légende.

Cette histoire de « meilleur cas, pire cas, cas moyen » est très utilisée pour parler de la complexité des algorithmes. On ne s’intéresse en général que peu au « meilleur cas », parce qu’en général, Murphy aidant, c’est rarement le cas qui arrive. (Même si on peut éventuellement se poser la question de « comment faire pour avoir le meilleur cas plus souvent ? » si ça peut faire une différence pour l’algorithme.) En général, on s’intéresse plutôt au cas moyen et au pire cas.

L’avantage de s’intéresser au pire cas, c’est que c’est le seul qui fournit des garanties. Si je dis que mon algorithme, dans le pire cas, s’exécute en tant de temps, je garantis qu’il ne sera jamais plus long que ça, même s’il lui arrive d’être plus rapide. Dans certains cas, on a besoin de ce genre de garanties. En particulier, on s’intéresse parfois (dans le domaine de la cryptographie en particulier) à ce qu’il se passe si un « adversaire » me fournit les données comme il veut, et de préférence de manière à compliquer ma vie le plus possible. Et on veut des garanties sur le fait que ce qu’on fait fonctionne comme on veut que ça fonctionne, même quand on a un adversaire en face qui fait tout pour nous pourrir la vie. L’inconvénient, c’est qu’on surestime souvent le temps d’exécution « usuel » si on prend en compte le pire cas, et qu’on peut se retrouver à le surestimer de beaucoup.

L’avantage de s’intéresser au cas moyen, c’est justement qu’on a une idée de ce qui se passe « normalement ». (Je fais beaucoup de raccourcis et je dis probablement des choses qui ne sont pas vraies dans le cas général, mais dans l’idée c’est pas si délirant que ça). Ça donne aussi une idée de ce qui se passe si on répète l’algorithme plusieurs fois sur des données indépendantes ; le temps moyen d’une exécution sera quelque part entre le meilleur cas et le pire cas. L’autre avantage de s’intéresser au cas moyen, c’est qu’il y a parfois des manières « simples » d’éviter au maximum le pire cas. Par exemple, si j’ai un adversaire qui me donne les livres dans un ordre qui me pourrit mon algorithme, je peux « compenser » ça par le fait de mélanger moi-même les livres au début pour que la probabilité d’être dans un « mauvais » cas soit faible (et ne dépende pas de ce que me fournit mon adversaire). L’inconvénient, c’est évidemment qu’on n’a aucune garantie sur le temps « maximum » que prend un algorithme.

Évidemment, ce qu’on fait au final dépend de ce qu’on veut faire (fou, non ?).

Ceci étant posé, les complexités, en nombre d’opérations, que j’ai données précédemment (2n-1, (n²+n)/2, (n²+9n)/4, 2n log(n)) ne sont pas celles qu’on utilise en général. Si on me demande les résultats précédents, je réponds que les complexités sont, respectivement, « n » (ou « linéaire »), « n² » (ou « quadratique »), « n² » et « n log n ». Ça peut paraître extrêmement approximatif et peu précis et tout ce genre de choses, et je dois dire que les premières fois que j’ai vu ce genre d’approximations, ça m’a agacée au plus haut point. Bon, le fait que c’était en cours de physique avait probablement un rapport avec ça, mais, bon. Depuis, je trouve que c’est drôlement pratique et même que ça a du sens. Il faut savoir, déjà, que le fait que « ça a du sens » a une justification mathématique solide. Je ne vais pas la donner ici, parce que c’est très nettement au-dessus du niveau du billet que je suis en train de vouloir écrire. Pour les gens intéressés, qui lisent l’anglais, et qui ont pas peur des trucs du genre « limite en plus l’infini de blah », il y a http://en.wikipedia.org/wiki/Big_O_notation (ou son pendant en français, http://fr.wikipedia.org/wiki/Comparaison_asymptotique, mais je trouve la version anglaise plus claire).

Bon, sinon, j’ai au moins deux trucs à tenter de justifier ici. Attention, ce que je vais faire ici est très, très peu rigoureux. La première question est celle de ce qui arrive aux « petits » termes. L’idée, c’est que je ne garde que ce qui « compte » dans le fait que mon nombre d’opérations augmente avec le nombre d’éléments à trier. Par exemple, si j’ai 750 livres à trier, et que je veux faire ça avec mon premier algorithme, dans le cas « moyen », j’ai (n²+9n)/4 opérations, c’est à dire n²/4 + 9n/4. Pour 750 livres, ces deux « morceaux » valent, respectivement, 140625 et… 1687. Si j’ai 1000 livres à trier, je monte à 250000 et 2250. Le premier « morceau » de l’expression est beaucoup plus gros, et il grandit beaucoup plus vite. Si je veux estimer le temps que ça me prend, sans avoir besoin de trop de précision, je peux prendre le n²/4 et laisser tomber le 9n/4 – déjà pour 1000 livres, le nombre d’opérations du 9n/4 correspond à moins de 1% du total.

La deuxième question est plus compliqué (à mon sens) : pourquoi est-ce que je considère identiques « n² » et « n²/4 », « 2 n log n » et « n log n » ? Encore une fois, il y a une justification mathématique derrière tout ça, que je vais tenter d’éviter de vous infliger. Mais on peut tenter de le justifier aussi en faisant de grands moulinets. (Je ne suis pas très satisfaite de mes explications ici, mais je ne trouve pas mieux. Si un Gentil Lecteur a mieux, qu’il n’hésite pas à expliquer dans les commentaires 🙂 ).

L’idée, c’est qu’on ne s’intéresse pas nécessairement à un algorithme « tout seul », mais à comparer différents algorithmes. Et, en particulier, on s’intéresse à la comparaison dite « asymptotique », c’est à dire à ce qu’il se passe quand on a un très grand nombre d’éléments en entrée de l’algorithme (par exemple un très grand nombre de livres à trier). Et si j’ai un très grand nombre de livres à trier, j’aimerais autant que ça me prenne le moins de temps possible, et donc je cherche le « meilleur » algorithme, celui qui va le plus vite.

Pour que ça me prenne le moins de temps possible, j’ai deux solutions. Ou bien je réduis le temps que chaque opération prend, ou bien je réduis le nombre d’opérations lui-même. Je prends mon algorithme 1, qui fait n²/4 opérations, et mon algorithme 2, qui fait 2 n log n opérations pour n éléments. Supposons que j’aie un ordinateur qui fait une opération en une seconde, et que je veuille trier 100 éléments. Avec le premier algorithme, ça lui prendra environ 2500 secondes. Avec le deuxième algorithme, ça lui prendra environ 1328 secondes (parce que 2*100*log(100) est environ égal à 1328). Maintenant, supposons que j’aie un ordinateur vachement plus rapide sur lequel faire fonctionner mon premier algorithme. Au lieu de prendre une seconde, cet ordinateur est cinq fois plus rapide et il peut effectuer une opération en un cinquième de seconde (0.2 seconde). Du coup, je peux trier mes 100 éléments en 0.2*100²/4 = 500 secondes, ce qui est plus rapide que ce que je peux faire avec l’autre ordinateur. Youpi. Mais il y a évidemment deux bémols à ça. Le premier bémol, c’est que si je mets mon deuxième algorithme sur le deuxième ordinateur aussi, je peux trier mes éléments en 0.2*2*100*log(100) = 265 secondes. Bon, supposons que pour une raison bizarre le deuxième algorithme ne fonctionne pas sur le deuxième ordinateur et qu’il faille que je le garde sur le premier ordinateur. Mais le deuxième bémol, c’est que si j’ai maintenant 1000 éléments à trier et non plus 100, ça va me prendre, avec le premier algorithme sur l’ordinateur vachement plus rapide, 0.2*1000²/4 = 50000 secondes, et avec le deuxième algorithme sur l’ordinateur vachement plus lent, 2*1000*log(1000) = 19931 secondes.

Et c’est un peu l’idée qu’il y a derrière la suppression des « nombres multiplicateurs » dans mon évaluation de complexité. Si j’ai un algorithme qui s’exécute avec une complexité « dans les n² » et un algorithme qui s’exécute avec une complexité « dans les n log n », je peux mettre l’ordinateur le plus puissant que je veux derrière le premier algorithme, il y aura toujours un nombre d’éléments pour lequel mon deuxième algorithme, même sur une machine très lente, ira plus vite que le premier. Le nombre d’éléments peut être très grand si la première machine est très rapide et la deuxième très lente, mais, comme je m’intéresse à ce qu’il se passe avec de très grands nombres d’éléments, c’est pas très grave.

Donc, quand je parle de comparer deux algorithmes, il est beaucoup plus intéressant de voir que j’en ai un dont le temps d’exécution est en n log n et un en n², que de pinailler sur la constante (le nombre) qui va devant le n log n ou le n².

Évidemment, pour deux algorithmes en n², on peut se poser la question de la constante qui va devant. En pratique, ça se fait assez peu, parce qu’à moins d’avoir des choses extrêmement simples et carrées (et encore), suivant la manière dont on implémente les choses (avec un langage de programmation), déterminer ladite constante devient très difficile. Il faut aussi se poser la question, exactement, de ce qu’est une opération. Il y a des modèles « classiques » qui permettent de définir tout ça, mais relier ces modèles aux langages de programmation actuels doit tenir à peu près de l’utopie.

Bon, et en tant que « gens qui font de l’algorithme », qu’est-ce qui nous plaît bien, qu’est-ce qui commence à nous faire grimacer, et qu’est-ce qui nous fait courir à toute vitesse dans l’autre sens ? Je donne tout ça en fonction de la « taille » de l’entrée, n ; pour mon exemple de tri, c’est le nombre d’éléments à trier. Si je fais des opérations sur des graphes, la taille de l’entrée va typiquement être le nombre de sommets du graphe, parfois le nombre d’arcs.

Les algorithmes « en temps constant » et « logarithmiques » (donc avec soit un nombre d’opérations constant, soit un nombre d’opération de type log n) sont relativement rares, parce qu’avec log n opérations (ou un nombre constant d’opérations), on n’a même pas le temps de regarder tout ce qu’on a en entrée. Donc, quand on trouve un algorithme de ce type, on est très très content. Un exemple « classique » d’algorithme qui fonctionne en temps logarithmique, c’est celui de chercher un élément dans une liste triée. Quand la liste est triée, on n’a pas besoin de lire toute la liste pour trouver l’élément qu’on cherche. On peut commencer par regarder s’il est avant ou après le milieu, regarder s’il est avant ou après le milieu de l’intervalle qu’on vient de redéfinir, et ainsi de suite. Je pourrais refaire une belle explication avec un arbre si ça vous intéresse, mais je vais pas faire ça maintenant.

On est aussi en général très content quand on trouve un algorithme linéaire (« n »). Ça veut dire, quelque part, qu’on lit tout ce qu’on a en entrée, on fait quelques opérations par élément, et paf c’est fini. n log n est aussi généralement considéré comme « acceptable ». C’est une borne importante, parce qu’on peut prouver que, dans les modèles algorithmiques courants (qui reviennent plus ou moins à compter des opérations « basiques »), on ne peut pas trier n éléments plus rapidement qu’en n log n opérations dans le cas général, c’est-à-dire sans rien savoir sur les éléments en question (Parce que si je sais qu’ils sont triés, ou dans l’ordre inverse, je peux les trier en temps linéaire). Du coup, il y a un certain nombre d’algorithmes qui s’appuient, à un moment ou un autre, sur un tri ; si on ne peut pas se débarrasser du tri, on ne peut pas non plus descendre en-dessous de n log n.

On commence à grommeler un peu à partir de n², n³, et à grommeler beaucoup sur les puissances supérieures de n. Les algorithmes qui peuvent s’exécuter en un temps $n^k$ , pour une valeur quelconque de k (y compris 1000000) sont appelés « polynomiaux ». L’idée, c’est que, de la même manière qu’un algorithme en n log n finira par être plus efficace qu’un algorithme en n², en prenant un entrée suffisamment grande, un algorithme polynomial, quel que soit k, finira par être plus efficace qu’un algorithme en $2^n$ . Ou même en $1.308^n$ . Ou même en $1.01^n$ .

Évidemment, en pratique, ce genre de raisonnement a ses limites aussi. J’ai un exemple qui m’amuse personnellement beaucoup, et j’espère qu’il vous amusera aussi. Considérons le problème de la multiplication de deux matrices entre elles. (Pour les gens qui n’ont pas jamais vu de matrices, on peut voir une matrice comme un tableau de nombres – et il se trouve qu’on peut multiplier ces tableaux de nombres. C’est un peu plus compliqué que de multiplier les nombres un par un, mais guère.) (Dit la fille qui savait pas comment multiplier deux matrices avant la 3e année d’école d’ingénieur, mais c’est une autre histoire.)

L’algorithme qu’on apprend à l’école permet de multiplier deux matrices en un temps n³, où on considère des matrices de taille n*n (pour les gens pas familiers des matrices : on trace un tableau de n lignes et n colonnes, et on met des nombres dedans). En se forçant un peu, on peut trouver un algorithme (algorithme de Strassen, de son petit nom), pas trop compliqué, qui fonctionne en un temps $n^{2.807}$ (ce qui est meilleur que le n³). Et en se forçant beaucoup, il existe un algorithme qui fonctionne en temps $n^{2.3727}$ (Coppersmith–Winograd et ses dérivés). C’est, je crois, le seul algorithme pour lequel j’ai entendu PLUSIEURS personnes faisant de la théorie dire que « oui, mais vraiment, la constante est vraiment dégueulasse » - en parlant du nombre par lequel on multiplie ce $n^{2.3727}$ pour avoir le temps d’exécution « réel ». Pour les raisons données précédemment, on ne connaît pas vraiment la constante en question, on sait juste qu’elle est dégueulasse. En pratique, de ce que je sais (peut-être que certains de mes lecteurs ont des avis plus tranchés sur la question), les algorithmes « rapides » de multiplication de matrice utilisent celui de Strassen (ou une variante), parce qu’à cause de la constante en question, les tailles de matrices pour lesquelles Coppersmith-Winograd serait « rentable » sont énormes, et peu utiles en pratique.

Voilà, sur cette anecdote amusante, je vais arrêter là pour ce billet. J’espère que c’était approximativement compréhensible, ce dont je ne suis pas vraiment sûre. N’hésitez pas à poser des questions, faire des remarques et tout ce genre de choses 🙂

Introduction à la complexité algorithmique – 1/2

Publié le 9 février 20139 novembre 2013 par Balise9 commentaires

Bon, ça y est, j’ai fini les deux billets qui savaient à peu près où ils allaient (un billet général sur l’informatique théorique, et un billet pour expliquer ce qu’est un logarithme parce que c’est toujours utile). Et après on a fait une petite pause, parce que bon. Donc maintenant je vais rentrer dans les choses un peu plus compliquées, et qui me sont plus difficiles à expliquer aussi. Donc j’écris, et puis on verra bien ce que ça donne à la fin. Ajoutons à cela que je veux essayer d’expliquer les choses en évitant au maximum le formalisme mathématique qui m’est maintenant « naturel » (mais croyez-moi, il a fallu me le rentrer dans le crâne à coups de marteau) : je sais vraiment pas ce que ça va donner. J’ai aussi décidé de couper ce billet en deux, parce qu’il est déjà fort long comme ça. Je pense que le deuxième sera plus court.

J’ai déjà défini un algorithme comme étant une suite bien définie d’opérations qui permettent d’arriver à un résultat. Je ne vais pas aller beaucoup plus loin dans la définition formelle, parce que je pense que ce n’est pas utile - du moins pas pour le moment. Et je vais définir, également de façon très peu formelle, la complexité algorithmique comme la quantité de ressources qu’il me faut pour exécuter mon algorithme. Par ressources, j’entendrai le plus souvent « le temps », c’est-à-dire le temps qu’il me faut pour exécuter un algorithme, parfois « l’espace », c’est à dire la quantité de mémoire (pensez-y comme à de la mémoire vive ou du disque dur) qu’il me faut pour exécuter mon algorithme.

Je vais prendre un exemple très classique pour illustrer mon propos, qui est celui du tri. Et pour donner un exemple concret de cet exemple classique, supposons que j’aie une bibliothèque pleine de livres. (Une supposition absolument et complètement folle.) Et qu’il me vienne l’idée sotte et complètement grenue de vouloir les trier, disons par ordre alphabétique de nom d’auteur (et de titre à nom d’auteur égal). Je dis qu’un livre A est « plus petit » qu’un autre livre B s’il doit être rangé avant dans la bibliothèque, et qu’il est « plus grand » s’il doit être rangé après. Avec cette définition, les bouquins d’Asimov sont plus petits que les bouquins de Clarke qui sont plus petits que les bouquins de Pratchett. Je vais garder cet exemple pendant tout le billet et je vais faire le parallèle avec les notions algorithmiques correspondantes.

Je commence donc par définir ce dont je parle. L’algorithme que j’étudie, c’est l’algorithme de tri ; c’est celui qui me permet de passer d’une bibliothèque en bordel à une bibliothèque rangée dans l’ordre alphabétique. En « entrée » de mon algorithme, c’est-à-dire les données que je donne à traiter à mon algorithme, j’ai une bibliothèque en bordel. En « sortie » de mon algorithme, j’ai les données traitées par mon algorithme, c’est-à-dire une bibliothèque rangée.

La première chose qu’on peut remarquer, c’est que plus on a de livres, plus c’est long à trier. Ça vient de deux choses. La première, c’est que si on considère une opération « élémentaire » du tri (par exemple, mettre le livre dans la bibliothèque), c’est plus long de faire ça 100 fois que 10 fois. La deuxième, c’est que si on considère tout ce qu’on fait pour chaque livre, plus il y a de livres, plus c’est long à faire. C’est plus long de chercher quel est le bon emplacement pour un livre parmi 100 que parmi 10.

Et voilà ce à quoi on s’intéresse ici : la manière dont le temps nécessaire à obtenir une bibliothèque rangée évolue en fonction du nombre de livres ou, de façon plus générale, la manière dont le temps nécessaire à obtenir une séquence triée d’éléments dépend du nombre d’éléments à trier.

Ce temps dépend de la méthode de tri qu’on utilise. Par exemple, on peut choisir une méthode de tri très très longue : tant que la bibliothèque n’est pas triée, on remet tout par terre et on met les livres dans un ordre aléatoire dans la bibliothèque. Pas trié ? On recommence. Ça, typiquement, ça va être très long. À l’autre bout du spectre, on a Mary Poppins : un Supercalifragilistic, et paf, la bibliothèque est rangée. La méthode Mary Poppins a d’ailleurs une particularité : elle ne dépend pas du nombre de livres à ranger. On dit que Mary Poppins s’exécute en « temps constant » : quel que soit le nombre de livres à ranger, ils seront rangés dans la seconde. En pratique, il y a bien une raison pour laquelle la méthode Mary Poppins fait rêver, c’est bien que c’est magique et difficilement réalisable en réalité.

Revenons, donc, à la réalité, et aux algorithmes de tri autres que Mary Poppins. Pour analyser la manière dont mon tri marche, je considère trois opérations élémentaires dont je peux avoir besoin pendant que je range :

comparer deux livres pour savoir si l’un se range avant ou après l’autre
mettre le livre dans la bibliothèque
et, en supposant que mes livres en bordel soient en bordel sur une table, le déplacement d’un livre sur la table.

Et je vais supposer aussi que ces trois opérations prennent le même temps, disons une seconde. Ça ne serait pas très efficace pour un ordinateur, mais je pense que c’est plutôt efficace pour un humain, et ça donne une idée. Je vais aussi supposer que ma bibliothèque est un peu magique, c’est-à-dire que ses rayonnages s’adaptent tous seuls et que les livres s’y placent sans avoir de problème de « rha, j’ai plus de place sur cette étagère, il faut que je descende des bouquins sur celle d’en-dessous, qui est pleine aussi, et là c’est le drame ». Pareil, ma table est magique, et déplacer un livre où je veux ne pose pas de problème. En pratique, il faudrait se poser ce genre de questions, y compris d’un point de vue algorithmique (quelle est la pénalité d’avoir à faire ça, est-ce que je peux l’éviter en étant malin). Mais comme je ne suis pas en train d’écrire un billet sur les tris mais sur la complexité algorithmique, je simplifie. (Et pour ceux qui savent de quoi je parle, oui, je sais que mon modèle est discutable. C’est un modèle, c’est mon modèle, je fais ce que je veux avec, et les explications restent valides dans mon modèle même s’il est discutable).

Un premier tri

Voici maintenant une première manière de trier. Je suppose que j’ai vidé ma bibliothèque en bordel sur ma table, et que je veux ranger les bouquins un par un. Le scénario suivant est assez peu réaliste pour un humain qui, probablement, se souviendrait approximativement de l’endroit où mettre le livre, mais essayez d’imaginer la situation suivante.

Je prends mon premier bouquin, je le mets dans la bibliothèque.
Je prends un deuxième bouquin, je compare avec le premier : s’il doit être rangé avant, je le mets devant, s’il doit être rangé après, je le mets après.
Je prends le troisième bouquin, je compare avec le premier. S’il doit être rangé avant, je le mets en première position. S’il doit être rangé après, je compare avec le deuxième bouquin que j’ai rangé. S’il doit être rangé avant, je le mets entre le bouquin 1 et le bouquin 2. S’il doit être rangé après, je le mets en dernière position.
Et ainsi de suite, jusqu’à ce que ma bibliothèque soit rangée. À chaque livre que j’insère, je compare, dans l’ordre, avec les livres déjà en place, et je l’insère entre le dernier livre qui est « plus petit » et le dernier livre qui est « plus grand ».

Et maintenant, je me demande combien de temps ça prend si j’ai, mettons, 100 livres, ou un nombre quelconque de livres. Je vais donner la réponse dans les deux cas : pour 100 livres et pour un nombre n de livres. Le temps pour n livres sera une fonction du nombre de livres, et c’est ce qui m’intéresse vraiment ici, ou plutôt ce qui m’intéressera vraiment dans le deuxième billet de cette introduction.

La réponse est que ça dépend de l’ordre dans lequel mes livres étaient au début quand ils étaient sur ma table. Il peut arriver, pourquoi pas, qu’ils étaient déjà triés. J’aurais peut-être dû vérifier ça avant de tout poser sur la table, ça aurait été plus malin, mais je n’y ai pas pensé avant. Il se trouve que c’est la pire chose qui puisse m’arriver avec cet algorithme, parce qu’à chaque fois que je veux ranger un livre, comme il est plus grand que tous ceux que j’ai rangés avant, il faut que je compare avec tous les livres que j’ai rangés avant. Comptons :

Je mets le premier livre dans la bibliothèque. Nombre d’opérations : 1.
Je compare le deuxième livre avec le premier livre. Je le mets dans la bibliothèque. Nombre d’opérations : 2.
Je compare le troisième livre avec le premier livre. Je compare le troisième livre avec le deuxième livre. Je le mets dans la bibliothèque. Nombre d’opérations : 3.
Je compare le quatrième livre avec le premier livre. Je compare le quatrième livre avec le deuxième livre. Je compare le quatrième livre avec le troisième livre. Je le mets dans la bibliothèque. Nombre d’opérations : 4.
Et ainsi de suite. À chaque fois que j’insère un livre, je le compare avec tous les livres qui l’ont précédé ; quand j’insère le 50e livre je fais donc 49 comparaisons, plus l’ajout du livre dans la bibliothèque, 50 opérations.

Donc pour insérer mes 100 livres, s’ils sont dans l’ordre au début, il me faut 1+2+3+4+5+…+99+100 opérations. Il se trouve, et je vais vous demander de me croire sur parole ici (c’est facile à démontrer, mais c’est pas l’objet) que 1+2+3+4+5+…+99+100, ça fait exactement (100*101)/2 = 5050 opérations. Et que, si je n’ai plus 100 livres, mais n livres qui se trouvent être dans l’ordre, il me faut n*(n+1)/2 = (n² + n)/2 opérations.

Supposons maintenant que mes livres étaient exactement dans l’ordre inverse duquel ils doivent être rangés. Ben cette fois ci, c’est la meilleure chose qui puisse m’arriver avec cet algorithme, parce que le livre que j’ajoute est toujours plus petit que tous ceux que j’ai rangés avant, donc il suffit de comparer avec le premier livre.

Je mets le premier livre dans la bibliothèque. Nombre d’opérations : 1.
Je compare le deuxième livre avec le premier livre. Je le mets dans la bibliothèque. Nombre d’opérations : 2.
Je compare le troisième livre avec le premier livre. Je le mets dans la bibliothèque. Nombre d’opérations : 2.
Et ainsi de suite : je compare toujours avec le premier livre, il est toujours plus petit, et j’ai toujours 2 opérations.

Donc si mes 100 livres sont exactement dans l’ordre inverse, je fais 1+2+2+2+…+2 = 1 + 99*2 opérations = 199 opérations. Et, si j’ai n livres dans l’ordre inverse, il me faut 1+2*(n-1) = 2n – 1 opérations.

C’est à partir d’ici que ça se corse un peu, parce que la situation devient moins bien définie, et que je vais commencer à faire des approximations dans tous les sens. J’essaie de justifier à chaque fois les approximations que je fais et pourquoi elles sont valides ; il est possible, cependant, que je zappe quelques étapes. N’hésitez pas à râler dans les commentaires si je suis complètement partie en sucette, parce que j’ai un peu de mal à me rendre compte

Je vais maintenant supposer que mes livres en bordel sont dans un état qui fait que, à chaque fois que j’ajoute un livre, il est inséré à peu près au milieu de ce qui a déjà été trié. (Je dis à peu près parce que si j’ai trié 5 livres, je vais typiquement ranger le 6e après le 2e ou après le 3e livre – les emplacements sont entiers, je vais pas le ranger après le 2.5e livre). Supposons que j’insère le livre numéro i ; j’estime le nombre de comparaisons que je fais à i/2 + 1, qui est supérieur ou égal au nombre de comparaisons que je fais effectivement. Pour voir ça, je distingue sur le fait que i soit pair ou impair. On peut montrer que ça marche pour tous les nombres ; je vais juste donner deux exemples pour expliquer qu’effectivement ça a de bonnes chances de marcher.

Si j’insère le 6e livre, j’ai 5 livres déjà rangés ; supposons que je veuille le ranger après le 3e livre (au « presque milieu »), je fais 4 comparaisons (parce qu’il est plus grand que le premier, deuxième, troisième livre, mais plus petit que le 4e) ; on a i/2 + 1 = 6/2+1 = 4.

Si j’insère le 7e livre, j’ai 6 livres déjà rangés, je veux le ranger après le 3e livre aussi (exactement au milieu), je fais également 4 comparaisons, et j’ai i/2+1 = 7/2 + 1 = 4.5.

Donc, je vais estimer le nombre d’opérations qu’il me faut pour ranger 100 livres, en comptant « large », et en me permettant des « demis-opérations ». Le but du jeu n’est pas ici de dénombrer exactement, mais d’avoir un ordre de grandeur, qui se trouvera être supérieur au nombre exact d’opérations.

Livre 1 : 1/2+1 = 1.5, plus le rangement, 2.5 opérations (je n’ai pas besoin de comparer, en fait, ici ; je le fais quand même parce que ça me facilite les calculs à la fin)
Livre 2 : 2/2 + 1 = 2, plus le rangement, 3 opérations (pareil ici, j’ai une comparaison de trop, parce que je n’ai qu’un seul bouquin de rangé, mais encore une fois je ne suis pas à un près).
Livre 3 : 3/2 + 1 = 2.5, plus le rangement, 3.5 opérations
Livre 4 : 4/2 + 1 = 3, plus le rangement, 4 opérations

Si je continue comme ça et que je range un peu mes calculs, j’ai, pour 100 livres, au plus

(1+2+3+4+…+99+100)/2 + 100 + 100 = (100*101/2)/4 + 200 = 2725 opérations.

Le premier élément de ma somme vient du « i/2 » que j’ai dans tous mes calculs de nombre de comparaisons. Le premier 100 vient du « 1 » que j’ajoute chaque fois que je compte les comparaisons (et je fais ça 100 fois), le deuxième 100 vient du « 1 » que j’ajoute à chaque fois que je compte le rangement des livres, et que je fais également 100 fois.

Ce 2725 est un peu surestimé, mais « de peu » : pour les deux premiers livres, j’ai exactement 2.5 comparaisons de trop ; pour les autres, j’ai au pire 0.5 comparaisons de trop. Sur 100 livres, ça fait donc au plus 98*0.5 + 2.5 = 51.5 opérations comptées en trop ; mon nombre exact d’opérations est donc compris entre 2673 et 2725. Il y aurait moyen de faire les choses un peu plus précisément, mais on verra par la suite (dans le prochain billet) pourquoi ça n’a pas grand intérêt.

Si je compte pour n livres, j’arrive à une estimation de (n*(n+1)/2)/2 + 2*n = (n²+9n)/4 opérations.

On peut montrer (mais pour le coup ça prendrait vraiment des proportions ici) que ce comportement est à peu près celui qu’on a quand on a des livres dans un ordre aléatoire. L’idée, c’est que si mes livres sont dans un ordre aléatoire, je vais en insérer certains plutôt au début, d’autres plutôt à la fin, et donc, « en moyenne », à peu près au milieu.

Une autre méthode de tri

Je vais maintenant expliquer une autre méthode de tri, qui est probablement moins facile à conceptualiser, mais qui je pense est la méthode la plus simple qui me permet de continuer mon argument.

Je vais supposer, cette fois, que je n’ai pas 100 livres à trier, mais 128. Parce que c’est une puissance de 2 et que ça me facilite la vie pour mon exemple concret. Et parce que j’y ai pas pensé avant et que j’ai la flemme de remonter dans mon exemple pour repartir sur 128 plutôt que 100.

Je suppose que tous mes livres sont sur la table, directement posés dessus, et je vais faire des « ensembles » avant de ranger mes bouquins dans la bibliothèque. Et je vais faire ces ensembles d’une façon un peu bizarroïde, mais efficace.

Je commence par combiner mes livres deux par deux. Je prends deux livres, je les compare, je mets le plus petit à gauche et le plus grand à droite. À la fin de cette opération, j’ai 64 ensembles de deux livres, avec dans chaque ensemble un petit livre à gauche et un grand livre à droite. Pour faire cette opération, j’ai dû faire, en tout, 64 comparaisons, et 128 déplacements de livres (je suppose que je déplace toujours les livres, ne serait-ce que pour les prendre en main et lire les auteurs/titres).

Ensuite, je prends mes ensembles de deux livres, et je les combine aussi de façon à avoir des ensembles de 4 livres, toujours ordonnées. Pour faire ça, je compare les deux premiers livres de deux ensembles, le plus petit des deux devient le premier livre de mon nouvel ensemble de 4. Je compare ensuite le livre restant de l’ensemble de 2 avec le premier livre de l’ensemble de 2, et je mets le plus petit en 2e position de mon ensemble de 4. Là, il peut se passer deux choses. Ou bien il me reste un livre dans chacun des ensembles initiaux ; auquel cas, je les compare, et je les mets dans l’ordre dans mon ensemble de 4. Ou bien il me reste un ensemble de deux ; je peux alors me contenter de les ajouter à la fin de mon ensemble de 4 et j’ai mon ensemble de 4. Voilà deux petits dessins qui distinguent les deux cas ; chaque carré représente un livre dont l’auteur a un nom commençant par la lettre indiquée, chaque rectangle représente mes ensembles de livres (les initiaux de 2 et le final de 4 livres), et les éléments rouges sont ceux qui sont comparés à chaque étape.

Bref, pour chaque ensemble de 4 que je crée, je dois faire 4 déplacements, et 2 ou 3 comparaisons. Je termine cette opération avec 32 ensembles de 4 livres ; donc au final je fais 32*4 = 128 déplacements et entre 32*2 = 64 et 32*3 = 96 comparaisons.

Je crée ensuite 16 ensembles de 8 livres, également en comparant le premier élément de chaque ensemble de livres et en créant un ensemble commun trié. Pour combiner deux ensembles de 4, il me faut 8 déplacements et entre 4 et 7 comparaisons. Je ne vais pas rentrer dans le détail de la manière d’obtenir ces chiffres ; la manière la plus simple avec ce genre de chiffres est d’énumérer tous les cas, ça commence à être fastidieux à 4, mais c’est encore gérable. Donc pour créer les 16 ensembles de 8 livres, il faut que je fasse 16*8 = 128 déplacements et entre 16*4 = 64 et 16*7 = 112 comparaisons.

Et je continue comme ça jusqu’à avoir 2 ensembles de 64 livres, que je finis par combiner (directement dans la bibliothèque pour gagner du temps) pour obtenir une bibliothèque rangée.

Bon, et combien de temps ça me prend cette affaire ? Je vais déjà commencer par donner une estimation pour 128 livres, et après je regarderai ce que ça donne pour n livres. Le plus pénible, ça ne surprendra personne, est d’évaluer le nombre de comparaisons quand on combine deux ensembles de livres. Je vais me permettre une approximation de plus pour dire que, si je veux combiner deux ensembles qui font chacun k éléments en un gros ensemble qui fait 2*k éléments, il me faut au plus 2*k comparaisons. Pour voir ça, on peut essayer de raisonner par énumération et faire une preuve propre et tout. J’avoue que j’ai pas le courage, d’autant plus que je sais où mon raisonnement va, et que je sais que j’ai pas envie de faire des calculs précis, parce qu’au final c’est pas très important d’être précis. On peut aussi faire l’observation suivante : à chaque fois qu’on fait une comparaison, on pose un bouquin dans le « gros » ensemble. Comme je ne pose que 2*k livres, je ne peux pas faire plus de 2*k comparaisons : si je faisais, par exemple, 2*k+1 comparaisons, il faudrait que je pose 2*k+1 livres… et je ne les ai pas. Donc, je vais estimer qu’à chaque fois que je combine deux ensembles de k éléments chacun en un ensemble de 2*k éléments, je fais au maximum 2*k comparaisons, et que je fais exactement 2*k déplacements. La deuxième observation, pour aller un peu plus loin et gagner encore un peu de temps dans les estimations, c’est qu’à chaque fois que je combine mes ensembles de k éléments en ensembles de 2*k éléments, je pose, en tout, exactement 128 livres (puisque c’est le nombre total de livres que j’ai, que chaque livre est dans un « petit » ensemble au départ et qu’il arrive dans un « grand » ensemble). Donc, je ne fais, au maximum, que 128 comparaisons à chaque étape.

Il me reste donc à compter le nombre d’étapes.

Pour 128 livres, ça me fait donc, au maximum :

Passer de 128 ensembles de 1 à 64 ensembles de 2 
Passer de 64 ensembles de 2 à 32 ensembles de 4
Passer de 32 ensembles de 4 à 16 ensembles de 8
Passer de 16 ensembles de 8 à 8 ensembles de 16
Passer de 8 ensembles de 16 à 4 ensembles de 32
Passer de 4 ensembles de 32 à 2 ensembles de 64
Passer de 2 ensembles de 64 à 1 ensemble de 128

Soit 7 étapes. Dans chacune de ces 7 étapes, j’ai 128 déplacements, et au maximum 128 comparaisons, soit au maximum 7*(128+128) = 1792 opérations. Notons que je n’ai fait ici aucune hypothèse sur l’ordre initial des livres. À comparer avec les 5050 opérations du « pire cas » du tri précédent, ou avec les environ 2700 opérations du cas « moyen » – nombres qui étaient d’ailleurs calculés pour 100 livres et pas 128 - pour 128 livres, on aurait, respectivement, 8256 opérations pour le « pire cas » et environ 4300 opérations pour le cas moyen.

Qu’en est-il exactement de la formule générale pour n livres ? Je pense qu’on peut être d’accord sur le fait que, à chaque étape, on déplace n livres, et qu’on fait au plus n comparaisons (puisque chaque comparaison correspond au fait de poser un livre). Donc, à chaque étape, je fais au plus 2*n comparaisons. La question est maintenant de savoir combien d’étapes on fait. Et c’est ici que mon splendide billet sur les logarithmes (kof) m’est utile. Est-ce que vous pouvez voir la similarité avec la figure suivante ?

Et si je dis que les feuilles de l’arbre sont les livres en bordel avant la première étape ? C’est plus clair ? (J’espère…). Au niveau d’au-dessus, les feuilles (livres) sont combinées en ensembles de deux, qu’on combine au niveau d’au-dessus en ensembles de quatre, etc… jusqu’à n’avoir qu’un seul ensemble qui contient tous les livres. Et le nombre d’étapes est précisément égal au logarithme (en base 2) du nombre de livres, ce qui correspond à la « profondeur » (le nombre de niveaux) de l’arbre en question.

Donc, pour conclure, pour n livres, j’ai, dans le modèle que j’ai défini, 2*n*log(n) opérations (où mon log est en base 2).

Voilà, je vais arrêter là pour ce premier billet. Dans le billet suivant, j’expliquerai pourquoi je ne me suis pas trop fatiguée à faire des calculs complètement exacts et pourquoi la phrase que je prononce probablement le plus souvent c’est « pff, c’est une constante, on s’en fout ». (Et peut-être aussi pourquoi des fois on s’en fout pas tant que ça 🙂 ). J’espère que c’était à peu près compréhensible jusqu’ici ; sinon, n’hésitez pas à râler, poser des questions, et tout ce genre de choses. Moi en tous cas je trouve ça rigolo d’écrire tout ça 🙂

Intuition mathématique

Publié le 8 février 20139 novembre 2013 par Balise6 commentaires

Je viens de commencer à rédiger un billet sur la complexité algorithmique, mais je me suis dit que celui-ci venait avant, parce que je ne suis pas à l’abri des tics de langages qui commencent à me venir : « intuitivement », « on voit bien que », « il est évident que ». Christophe m’a d’ailleurs fait remarquer que mon « ça me paraît assez clair » du billet sur les logarithmes (je crois que j’en ai au moins deux) n’était pas forcément des plus heureux. J’avais commencé par intituler ce billet « Compréhension, intuition et créativité », je crois que je vais me limiter au deuxième, parce que ça fait déjà un billet d’un fort beau gabarit ma foi.

J’essaie autant que possible, quand j’explique, d’éviter « l’argument d’intuition », parce que ça m’angoissait pas mal au début quand on me l’offrait et que, justement, je nageais pas mal à comprendre pourquoi c’était intuitif. Notons au passage que ça m’est encore arrivé l’autre jour en examen, de me vautrer sur le « pourquoi c’est intuitif ». Un truc qui me paraissait tellement lumineusement évident que j’en oubliais la raison profonde pour laquelle c’était évident. C’est assez agaçant quand on te le fait remarquer… surtout quand « on » est un examinateur. Mais je m’égare.

Un des articles les plus intéressants que j’ai lus sur le sujet est un article de Terry Tao, There’s more to mathematics than rigour and proofs (et oui, les plus observateurs remarqueront qu’il est en anglais 🙂 ). Il y distingue trois « stades » dans l’éducation mathématique :

le stade « pré-rigoureux » : on fait beaucoup d’approximations, d’analogies, et probablement plus de calculs que de théorie
le stade « rigoureux » : on essaie de faire les choses proprement, de façon précise et formelle, et on manipule des objets abstraits sans avoir forcément de compréhension profonde de ce qu’ils représentent (mais on les manipule correctement)
le stade « post-rigoureux » : on connaît suffisamment son domaine pour savoir quelles approximations et quelles analogies sont effectivement valides, on a une bonne idée rapidement de ce qu’un truc va donner quand on aura fini la preuve/le calcul, et on comprend effectivement les concepts qu’on manipule.

Je m’estime à peu près dans un mélange des trois niveaux 🙂 Je commence à avoir une certaine « intuition » (je reviendrai sur ce que je mets là-dedans), mais j’ai toujours autant de mal à mener un calcul proprement. Et, évidemment, ça dépend des domaines : dans mon domaine, je suis à peu près là ; si on me demande là tout de suite de résoudre des équadiff ou de faire de l’analyse qui tache, je vais probablement me sentir au stade pré-pré-rigoureux :)

Donc, de mon point de vue, les catégories sont évidemment plus fluides que ça, mais je crois que le message est le bon. Et qu’il faut pas paniquer quand la personne en face dit « il est évident/intuitif que » : c’est juste qu’elle a plus de pratique. Et qu’il est parfois difficile d’expliquer ce qui est devenu, avec la pratique, évident. Si je dis « il est évident que 2+3=5 », on sera probablement tous d’accord là-dessus ; si je demande « oui mais pourquoi 2+3=5 ? », on finira bien par me répondre, mais je m’attends à un blanc d’au moins quelques secondes avant ça. Je caricature un peu, mais je crois que c’est à peu près l’idée.

Dans le langage courant, l’intuition a quelque chose de magique, de « je sais pas pourquoi, mais je crois que les choses sont comme ci ou comme ça et qu’il va se passer ci ou ça ». J’ai tendance à me méfier pas mal de l’intuition dans la vie courante, parce que j’ai tendance à me méfier de ce que je ne comprends pas. En maths, la définition est à peu près la même : « je crois que le résultat va avoir cette gueule là, je sens bien que si je déroule cette preuve ça va marcher ». L’avantage de l’intuition mathématique, c’est qu’on peut la vérifier, comprendre pourquoi elle est juste, ou pourquoi elle est fausse. Dans mon expérience, l’intuition - juste - (ou ce qu’on met derrière ce mot) vient surtout avec la pratique, avec le fait d’avoir vu différentes choses, avec le fait d’avoir étudié pas mal, avec le fait de relier les choses les unes aux autres. Je pense que ce qu’on met derrière le mot « intuition », c’est le fait de relier quelque chose de nouveau (un nouveau problème) à quelque chose qu’on a déjà vu, et de faire ça correctement. C’est aussi le fait de reconnaître des « schémas » (j’utiliserais le mot « pattern » si j’écrivais en anglais). Dans le domaine de la complexité algorithmique, qui est le sujet du prochain billet en projet, c’est « je pense que cet algorithme va me prendre tant de temps, parce qu’au final c’est la même chose que celui-là qui est super connu et qui prend tant de temps ». Le truc, c’est que les associations ne sont pas toujours « conscientes » : on se retrouve à voir le résultat d’abord, et à l’expliquer après.

Ça n’empêche évidemment pas de se planter dans les grandes largeurs. Penser qu’un problème va prendre beaucoup de temps à résoudre (algorithmiquement parlant), alors qu’en fait il y a une condition qui le rend facile. Penser qu’un problème n’est pas très difficile, et se rendre compte qu’en fait il va prendre plus de temps que ce que l’on pensait. Enfin, en tous cas, à moi ça m’arrive toujours. J’estime le fait de me planter comme un progrès par rapport à l’étape précédente qui était « mais comment peut-on avoir une quelconque idée sur le sujet ? ».

Je ne sait pas comment se développe cette intuition. Je sais que la mienne est dans un bien meilleur état que ce qu’elle était il y a un an et demi. C’est suffisamment récent pour qu’il m’arrive encore de m’émerveiller sur le fait que des choses sur lesquelles je nageais à l’époque me paraissent maintenant assez naturelles.

C’est aussi suffisamment récent pour que je me rappelle l’angoisse de pas comprendre pourquoi ça peut être intuitif pour certaines personnes. Alors, promis, je vais essayer d’éviter. Mais j’aimerais bien que si jamais ça m’échappe vous me le fassiez remarquer, surtout si ça vous pose problème. Accessoirement, il y a de bonnes chances que si je dis « c’est intuitif », c’est parce que j’ai la flemme de partir dans des explications qui me semblent évidentes (mais qui ne le seraient peut-être pas pour tout le monde). Donc, voilà, je vais essayer de ne pas avoir la flemme 🙂

Et donc, c’est quoi un logarithme ?

Publié le 6 février 20138 janvier 2019 par Balise14 commentaires

Je soupçonne que je vais avoir besoin, dans ma série d’articles d’informatique théorique, de logarithmes. Pourquoi ? Parce que c’est une des fonctions « utiles » lorsque l’on parle de complexité algorithmique. Donc, pour être sûr que tout le monde soit sur la même page, je fais un cours de rattrapage sur les logarithmes. Les gens qui ont de mauvais souvenirs de leurs maths de lycée ont probablement aussi de mauvais souvenirs des logarithmes, et pourtant, les logarithmes, c’est chouette.

En parlant de logarithmes, je ne sais pas comment ils ont été introduits dans vos cours de maths respectifs ; pour ma part, je suis à peu près sûre qu’on me l’a défini à partir de l’intégrale de la fonction inverse. RESTE ICI, C’EST PAS CE QUE JE VAIS FAIRE. Enfin pas tout de suite. Je vais commencer par essayer de donner une intuition du bidule.

Considérons la figure que je viens d’insérer avec brio dans mon billet. Je suis partie d’un point, à partir de ce point j’ai fait deux branches, au bout desquelles j’ai ajouté un point ; sur chacun de ces points, j’ai ajouté deux branches, au bout desquelles j’ai ajouté un point, et ainsi de suite. J’aurais pu continuer comme ça longtemps, conceptuellement – je vais avoir des problèmes de place et des problèmes de fatigue (ça va être pénible très vite d’ajouter des ptits points), mais conceptuellement, je pense qu’on peut tous imaginer un arbre comme celui-ci avec autant de niveaux qu’on le souhaite. Supposons aussi, parce qu’on fait de l’informatique, que la « racine » de l’arbre (le tout premier point que j’ai ajouté sur ma figure) soit au niveau 0. Si je « retourne » l’arbre, ça peut avoir une certaine logique, c’est le « rez-de-chaussée », et le niveau suivant est le « premier étage ». Supposons maintenant que je veuille compter le nombre de « feuilles » de mon arbre, c’est-à-dire le nombre de points que j’ai sur le dernier niveau de mon arbre.

Il est assez clair que le nombre de feuilles dépend du niveau auquel j’arrête mon arbre, et qu’il augmente à chaque niveau. Si je m’arrête au niveau 0, j’ai 1 feuille. Si je m’arrête au niveau 1, je multiplie ça par deux (parce que je fais deux branches), ça fait 2. Si je m’arrête au niveau 2, je multiplie le nombre de feuilles du niveau 1 par deux encore, ça fait 4. Et à chaque niveau, je prends le nombre de feuilles du niveau précédent et je le multiplie encore par deux. Au niveau 3, j’aurai donc 2*2*2 = 8 feuilles et, au niveau 4, 2*2*2*2 = 16 feuilles. Pour connaître le nombre de feuilles au niveau numéro $n$ , où $n$ est le numéro de mon niveau, je fais $n$ multiplications de 2 par lui-même, ce qui s’écrit $2^n$ (et se lit « deux à la puissance $n$ »).

Supposons à présent que je ne veuille pas connaître le nombre de feuilles correspondant à un niveau, mais le nombre de niveaux correspondant à un nombre de feuilles donné. Par exemple, j’ai 2 feuilles : ça correspond au niveau 1. 16 feuilles : ça correspond au niveau 4. Si j’en ai 32, ça correspond au niveau 5. Et si j’ai 128 feuilles, ça correspond au niveau 7. Bon, évidemment, ça se complique un peu si j’ai, mettons, 20 feuilles. 20 feuilles, ça correspond à un niveau « 4 et des poussières » – j’ai dessiné jusqu’au niveau 4, j’ai commencé à dessiner le niveau 5, et j’ai eu la flemme de finir. Cette opération, qui est l’opération réciproque de l’opération précédente, c’est un logarithme. Je dis que c’est l’opération réciproque, parce qu’elle me permet de « défaire » l’opération précédente. Je prends un nombre $n$ , j’en prends la puissance de 2, ça me donne $2^n$ , et si je reprends le logarithme de ça, j’ai

$\log(2^n)= n$

De la même manière, si j’ai un nombre $n$ , que j’en prends le logarithme, et que j’en reprends la puissance de 2, j’ai

$2^{\log n} = n$

Bon, c’est bien gentil, tout ça, mais qu’est-ce qu’il se passe, si au lieu de faire deux branches à chaque étape, j’en fais 3 ? Selon le même raisonnement que précédemment, au niveau $n$ , j’ai 3*3*…*3 feuilles, c’est à dire $3^n$ . Et, bon, ben de la même manière, je peux définir un logarithme qui soit la réciproque de ce $3^n$ . Mais, bon, je veux pouvoir les distinguer – donc je mets la puissance à laquelle ils correspondent en indice, comme ceci :

$\log_2$ , $\log_3$

avec

$3^{log_3 n} = n$

$\log_3(3^n) = n$

L’indice de mon logarithme, on appelle ça la « base » du logarithme. J’en profite pour faire une petite remarque sur le logarithme en base 10 (c’est aussi valable pour les autres bases, au moins entières, de logarithmes, mais je ne rentre pas là-dedans). Il est très facile d’avoir une évaluation « à la louche » du logarithme en base 10 d’un nombre. C’est le nombre de chiffres du nombre en question, moins 1. On a $\log_{10}(10) = 1$ , $\log_{10}(100) = 2$ (parce que $10^2 = 100$ ); tous les nombres entre 10 et 100 ont un logarithme en base 10 entre 1 et 2. De la même manière, on peut estimer que le logarithme en base 10 de 14578 est entre 4 et 5. Pour voir ça, il suffit de voir que 14578 est compris entre $10000 = 10^4$ et $100000 = 10^5$ , ce qui permet de conclure sur la valeur du logarithme. (Je passe un certain nombre de choses sous le tapis ici, en particulier les raisons qui font qu’on peut effectivement conclure ça.)

Bon, cela dit, maintenant que j’ai défini des bases de logarithme, qu’est-ce qui m’empêche d’utiliser des bases « exotiques » pour mes logarithmes ? La réponse est « rien ». Je peux définir un logarithme en base 3.5 (qui correspond à la puissance à laquelle j’élève 3.5 pour obtenir le nombre dont je prends le logarithme en base 3.5), $\frac 5 3$ (qui correspond à la puissance à laquelle j’élève $\frac 5 3$ pour obtenir le nombre dont je prends le logarithme en base $\frac 5 3$ ), ou même $\pi$ (qui correspond à… bon, ça ira, peut-être) si ça me chante. C’est moins « intuitif » si je considère mon explication avec les arbres et le nombre de niveaux (parce que c’est difficile de faire $\pi$ branches), mais en considérant la réciproque des fonctions puissance, ça me paraît raisonnablement clair.

La question suivante qu’on peut se poser, c’est si tous ces logarithmes en différentes bases ont un lien entre elles, ou plus exactement si on peut les exprimer d’une façon commune. La réponse est « oui ». C’est ici que j’introduis le logarithme népérien, aussi appelé logarithme naturel, dénoté $\ln$ . Le logarithme népérien est un logarithme en base $e \approx 2.71828$ . On peut exprimer n’importe quel logarithme dans n’importe quelle base $a$ comme ceci :

$\log_a(x) = \frac{\ln x}{\ln a}$

Ce qui veut aussi dire qu’on peut passer d’un logarithme d’une base $a$ à un logarithme d’une base $b$ comme ça :

$\log_a(x) = \frac{\ln x}{\ln a} = \frac{\ln x}{\ln b} \times \frac{\ln b}{\ln a} = \frac{\ln b}{\ln a}\log_b(x)$

(Et oui, c’est typiquement le genre de chose que j’ai dans mon formulaire d’examen, parce que je me souviens jamais dans quel sens c’est !)

L’important à retenir, ici, c’est que tous les logarithmes sont égaux « à une constante près » ; ils ont le même « comportement asymptotique » (j’introduis les termes ici, mais je ferai un billet spécifique sur le sujet, parce que c’est un peu long à expliquer). C’est intéressant dans le domaine qui nous préoccupe ici, parce qu’on s’intéresse surtout à l’estimation des comportements « à une constante près » quand on parle de temps d’exécution ou d’occupation mémoire d’un algorithme. Encore une fois, j’y reviendrai – prenez ça comme un « spoiler » des prochains épisodes 🙂

J’en arrive à la relation entre le logarithme népérien et la fonction inverse. Formellement, on écrit que

$\ln(x) = \int_1^x \frac 1 t \text{d}t$

Et voilà ce que ça veut dire, graphiquement :

La courbe rouge est la courbe de la fonction $x \mapsto 1/x$ . La zone grise correspond ici à l’intégrale de 1 à 6 ; l’aire de cette zone est égale à ln(6). Et on peut représenter le logarithme népérien de n’importe quelle valeur (supérieure à 1) par l’aire de la surface située entre l’axe des $x$ et la courbe $x \mapsto 1/x$ , prise entre 1 et cette valeur. Remarquons au passage que cette aire est égale à 1 lorsqu’on la considère entre 1 et e, e étant la base du logarithme népérien (parce que ln(e) = 1).

Et pour finir, une propriété intéressante de la fonction logarithme : on peut écrire (dans n’importe quelle base du logarithme)

$\log(a \times b) = \log(a) +\log (b)$

$\log(a/b) = \log(a) - \log(b)$

En tant que réciproque de la fonction puissance, c’est assez clair de voir ça. Étant entendu que si deux puissances d’un même nombre sont égales, alors l’exposant l’est aussi, on a d’une part :

$2^{\log_2(a \times b) } = a \times b$

et d’autre part

$2^{\log_2 a + \log_2 b} = 2^{\log_2 a}\times 2^{\log_2 b} = a \times b$

On peut dériver la deuxième égalité de la même manière – hop, exercice 😛

Notons au passage que c’est à cause de ce genre de propriété que les logarithmes ont été utilisés au départ. Si on a une grosse table avec plein de correspondances « nombre/logarithme », et qu’on veut multiplier deux nombres facilement, on regarde dans la table les logarithmes des deux nombres, on les ajoute (ce qui est vachement plus facile que de les multiplier), et on regarde la valeur correspondante du logarithme (on utilise la table dans l’autre sens) pour avoir la valeur des deux nombres initiaux multipliés. Historiquement, ce genre de tables est apparu au XVIIe siècle (on remerciera M. Napier) pour faciliter les calculs astronomiques ; la règle à calcul fonctionne également sur ce principe ; et tout ça n’a été détrôné que par l’arrivée, plutôt récente, des machines à calculer et des calculatrices…

Bref, les logarithmes, c’est cool. Et j’espère que vous en êtes à présent aussi persuadés que moi 🙂

« Et donc, tu fais quoi en ce moment ? » « De l’informatique théorique. Des maths, en gros. »

Publié le 5 février 20139 novembre 2013 par Balise15 commentaires

Ça fait quelques jours que j’ai envie d’écrire des choses un peu plus consistantes que « oh j’ai lu ça, c’était cool ». Plus spécifiquement, il y a une question qu’on me pose relativement souvent : « Et donc, tu fais quoi en ce moment ? ». J’ai beaucoup de mal à y répondre – en général je réponds quelque chose du genre « de l’informatique théorique. Enfin des maths, en gros ». C’est pas très satisfaisant, mais rentrer dans les détails quand on me pose une question « sociale » n’est pas forcément une bonne idée non plus. Mais peut-être qu’il y a des gens qui seraient intéressés par un peu plus de détails, et d’une façon que je pourrais expliquer à quelqu’un qui ne baigne pas dans le domaine depuis un an et demi. Pour donner une idée, j’essaie de viser un niveau « j’ai pas fait de maths depuis le lycée ». Je sais pas trop si je vais y arriver, ça commence à faire un bout de temps que j’ai quitté le lycée, et j’ai fait des maths depuis 🙂

Je vais donc commencer par rédiger un billet très général (celui-ci) pour poser un peu quelques bases ; et après, j’ai la ferme intention de rentrer dans les détails un peu plus. L’idée, c’est que je trouve vachement cool ce que j’étudie en ce moment ; et j’aimerais bien expliquer pourquoi je trouve ça vachement cool. Ça va demander un peu de boulot ; j’hésite limite à faire un premier billet sur « mais, mais, mais… c’est QUOI, un logarithme ? », parce que quand même les logarithmes c’est super utile, mais j’ai peur de faire une insulte à la culture scientifique de mes lecteurs. Je crois que je vais le faire quand même, parce que ça m’amuse moi, et que c’est quand même la raison principale de faire des choses. Et après, je compte faire des billets plus ou moins selon l’humeur du moment. Probablement un peu de complexité, probablement des graphes (j’aime bien les graphes), probablement un peu de probabilités (haha), et les « prérequis » pour tout ça (je suis en train de réfléchir à ce qu’il me faut pour un billet expliquant P/NP, ce qu’est un problème NP-complet, et la grande question de savoir si P = NP, je ne suis pas la première à me frotter à ce genre de billet, mais je pense que l’exercice didactique est intéressant 🙂 )

Je digresse déjà, c’est pas gagné. Revenons à nos moutons. Je suis actuellement en master d’informatique, spécialisation informatique théorique, de l’ETH à Zürich. Les modalités « usuelles » sont de faire 60 crédits de cours, généralement en deux-trois semestres, suivis d’un semestre de projet de recherche (avec rapport et soutenance à la fin, classique). Il se trouve que j’ai pris des chemins un peu détournés pour mon master, et que de fait je vais rentrer dans mon 4e semestre de cours, mais c’est pas vraiment la question ici.

« Mais c’est quoi, l’informatique théorique ? » seriez-vous peut-être tentés de me demander. La première réponse qui me vient à l’esprit, c’est que c’est la théorie de tout ce qu’on peut faire avec un ordinateur. Au cœur de tout ça, il y a la notion d’algorithme. Un algorithme, c’est simplement une suite d’instructions. On peut par exemple penser à une recette de cuisine comme à un algorithme :

Pour faire de la béchamel, il me faut du beurre, de la farine et du lait.
Mesurer des quantités égales de beurre et de lait.
Dans une casserole à feu moyen, faire fondre le beurre et y incorporer la farine jusqu’à obtenir une pâte épaisse.
Tant que la béchamel n’a pas la consistance souhaitée, ajouter du lait et mélanger.
Si on le souhaite, ajouter du sel, du poivre, de la muscade ou du fromage râpé.

On a une suite d’instructions (qui sont numérotées), qui peuvent être répétées (tant que la béchamel n’a pas la consistance souhaitée) ou qui ne sont exécutées que dans certaines conditions (on n’ajoute de la muscade que si on le souhaite).

De façon plus « classique », on peut aussi penser à l’algorithme de la division que tout le monde étudie à l’école primaire.

Je suis un peu biaisée sur les catégories de ce qu’on peut faire rentrer dans l’informatique théorique, parce qu’il y a des domaines que je connais bien mieux que d’autres, mais en voici une liste explicitement non exhaustive (si j’oublie votre domaine favori… c’est que je ne sais pas quoi en dire, n’hésitez pas à expliquer en commentaire). Pour une liste un peu plus complète, je vous renvoie sur l’article correspondant de la Wikipedia : Informatique théorique, qui reprend lui-même la liste de SIGACT (une grosse société savante du domaine, en gros). Quant au fait que « je fais des maths », l’informatique théorique est souvent considérée comme une branche des maths discrètes ; et en pratique, prouver qu’un truc marche implique de faire de jolies preuves pleines de jolies maths 🙂 (Ou de moches maths, mais c’est nettement moins satisfaisant.)

Je me permets un certain nombre d’approximations ici (en particulier je fais la confusion entre un problème et une instance d’un problème), j’essaie de faire simple sans faire de paragraphe à rallonges. Ceux qui savent de quoi je cause corrigeront d’eux-mêmes ; pour les autres : c’est une première approximation, qui n’est par définition pas exacte, mais que j’ai l’intention d’affiner dans les billets qui suivront.

L’algorithmique. Étant donné un problème, comment le résoudre avec un algorithme, comment prouver que la méthode de résolution (l’algorithme) qu’on propose est effectivement correcte, et combien de temps faut-il pour avoir un résultat ?
La théorie de la complexité. Ça inclut, mais pas seulement, le point « combien de temps il faut pour avoir un résultat » du point précédent. On s’intéresse aussi ici à la question : étant donné un problème, quel est le temps minimum et la consommation de mémoire minimum qu’il me faut pour le résoudre ?
La théorie des graphes. Un graphe est une structure mathématique composée de points (les « sommets » du graphe) et de traits (les « arcs » du graphe). Un exemple de graphe pourrait être la carte d’un réseau de métro : les stations sont les sommets, les arcs sont les connexions d’une station à une autre par une ligne de métro. En théorie des graphes, on s’intéresse aux propriétés de ces graphes (par exemple : est-ce que je peux aller d’un point à un autre ; quel est le plus court chemin d’un point à un autre ; si je supprime ce sommet là (ou, dans l’analogie précédente, si je ferme ma station de métro), est-ce que je peux toujours aller de mon point A à mon point B), et aux algorithmes pour décider ces propriétés (comment je fais pour déterminer quel est le plus court chemin d’un point à un autre du graphe).
Les structures de données. Comment stocker les données du problème qu’on cherche à résoudre, de la façon la plus efficace possible (en temps et en mémoire) pour le problème en question ? Ou, pour reprendre mon exemple précédent, comment stocker la carte du réseau de métro pour faire des calculs dessus ?
La géométrie algorithmique. Comment représenter et résoudre avec un ordinateur des problèmes qui touchent à la géométrie ? Un exemple typique est celui du « bureau de poste » : étant donné l’emplacement de tous les bureaux de poste d’une ville, comment déterminer efficacement celui qui est le plus proche de ma maison ? Si je ne cherche que celui qui est le plus proche de ma maison, je peux calculer la distance entre ma maison et tous les bureaux de poste ; mais comment faire ça plus efficacement si je cherche à définir, pour toutes les maisons de la ville, le bureau de poste le plus proche ? Et qu’est-ce que je fais si je veux ajouter/supprimer un bureau de poste ?
L’impact de l’aléatoire dans tout ça – pour certains algorithmes, il est intéressant d’ajouter une part de hasard dans les calculs (je lance une pièce, si elle fait pile mon algorithme fait ceci, si elle fait face mon algorithme fait cela). Quel impact ça a sur les algorithmes – en particulier sur le fait qu’ils renvoient le résultat correct ou non, et comment évaluer le temps nécessaire à résoudre (correctement) un problème avec un algorithme aléatoire ? L’étude de certaines structures aléatoires a aussi un intérêt en soi. On peut par exemple définir des graphes aléatoires : on prend un ensemble de points, et on ajoute un arc entre deux points selon une certaine probabilité. Selon la manière dont on définit un graphe aléatoire, il peut s’avérer un assez bon modèle d’un graphe de réseau social (qui est ami avec qui)… ou du cerveau humain.
La cryptographie. Si Alice veut envoyer un message à Bob en étant sûre qu’Ève ne puisse pas le lire, et si Bob veut être sûr que le message qu’il vient de recevoir provient bien d’Alice, comment faire ? Et surtout, comment prouver qu’effectivement Ève ne peut pas lire le message, et que Bob peut être sûr de la provenance du message ?
[EDIT] La calculabilité, comme on me le signale en commentaire. Il se trouve qu’on ne peut pas tout résoudre avec un algorithme, et qu’on peut même prouver que certaines choses ne peuvent pas être être calculées avec un algorithme. L’exemple le plus célèbre est celui du « problème de l’arrêt », c’est un peu méta, mais j’espère que vous me le pardonnerez. On peut prouver qu’il n’existe pas de programme qui décide si un programme donné finit par s’arrêter et à renvoyer un résultat. La preuve est jolie, même si elle fait un peu mal au crâne la première fois qu’on y est confronté ; j’en ferai peut-être un prochain billet 🙂

Voilà, tout ça, c’est des trucs dans lesquels j’ai au moins des notions de base. L’informatique théorique regroupe encore pas mal de choses dans lesquelles mon niveau de connaissance est à peu près nul : la théorie de l’information (à ma grande honte), l’apprentissage automatique (ou comment réussir à faire reconnaître des photos de chat à un ordinateur), les méthodes formelles (ou comment réussir à prouver que mon programme n’a pas de bug), l’informatique quantique (sait-elle mieux reconnaître une photo de chat que l’informatique classique), la bio-informatique (comment déterminer si deux séquences ADN sont proches ou non) et j’en oublie encore probablement un peu.

Notons accessoirement que faire rentrer ceci ou cela dans le domaine de l’informatique théorique peut toujours prêter à débat. Je ne suis par exemple pas convaincue de la présence de l’apprentissage automatique dans l’informatique théorique, parce que ça me paraît encore très expérimental (on a modifié ce paramètre là et par conséquent l’ordinateur reconnaît 2.2% de plus de chats). La Wikipedia parle d’informatique distribuée et concurrente (l’art d’utiliser plusieurs ordinateurs à la fois pour exécuter des programmes) comme faisant partie de l’informatique théorique. Je suis d’accord que l’intersection n’est pas nulle – mais je ne considérerais pas l’informatique distribuée comme un sous-ensemble de l’informatique théorique. Idem pour la bio-informatique ; certains éléments en font partie (l’exemple des chaînes ADN par exemple), mais je ne suis pas sûre que tous les bio-informaticiens se définissent comme des informaticiens théoriques 🙂

Je pensais que ce billet serait relativement court ; je crois que c’est un échec cuisant de ce point de vue. J’espère qu’il était cependant vaguement intéressant ; et s’il y a des choses que vous pensez que je peux traiter dans un futur billet de cette catégorie… ben n’hésitez pas 🙂

Ma guitare namoi

Publié le 30 janvier 2013 par Balise19 commentaires

Ça doit faire deux ans, à peu près, que j’ai commencé à faire joujou avec une guitare. Je dis deux ans, parce qu’il y a à peu près deux ans sur Twitter, je râlais que le A (l’accord) (me demandez pas la correspondance française, j’en sais rien) était ma nouvelle Némésis – et si je me souviens bien ça doit être à peu près le 3e accord que j’ai appris à jouer.

J’ai commencé à bricoler un peu par moi-même, avec une guitare électrique que Steve m’avait prêtée ; au début, je sortais le son sur la chaîne du salon ; c’était pas super optimal, mais, bon. J’ai acheté quelques bouquins, et j’ai bricolé pendant 4-5 mois, je dirais.

Le 24 juin 2011, j’ai pris ma première leçon de guitare 🙂 (Pour la date, j’ai été rechercher dans mon archive Twitter – ils ont par ailleurs bien fait les choses sur l’exportation et la recherche…). Et une semaine après, ayant entendu la différence que ça faisait d’avoir un vrai ampli plutôt qu’une chaîne au cul de la guitare, j’ai acheté un petit ampli rouge choupi (un Roland Microcube). Peu de temps après, Steve s’est racheté une guitare acoustique – une Washburn tout à fait sympathique, et il me l’a prêtée pendant un bon moment, en parallèle à l’électrique. J’ai joué avec les deux, et… Ben au final, j’ai trouvé que l’acoustique avait, paradoxalement, plus de polyvalence que l’électrique. Je sais pas trop comment expliquer ça. Probablement par le fait que tu PEUX faire des solos de ouf sur une acoustique, mais que gratouiller Kumbaya au coin du feu (je fais dans l’appel à l’imaginaire collectif, là), ben ça marche pas très bien avec une électrique.

Il y a un tout petit peu moins d’un an, j’ai acheté ma première guitare. Une acoustique, une Tanglewood Nashville III TD8. Je me suis sentie un peu ridicule dans le magasin, à tester des guitares avec trois accords et deux exercices de base – et à avoir la mâchoire qui se décroche en voyant le vendeur accorder la guitare en 20 secondes chrono sans accordeur 😉 (Je sais toujours pas accorder à l’oreille, d’ailleurs.) Mais le truc qui m’a le plus étonnée, c’était d’avoir un avis sur ce que j’aimais bien et sur ce que je n’aimais pas. Je m’étais dit que si la Washburn était toujours disponible, je prendrais la même – bon, c’était pas le cas, donc j’ai testé. Et j’ai craqué sur la Tanglewood, qui m’a paru avoir un son clair, propre et presque « girly » – ce qui ne veut STRICTEMENT rien dire, mais c’est l’impression que j’ai eue.

Je suis rentrée à la maison en faisant un câlin à la boîte dans le tram. (Vraiment.)

Quelques mois plus tard, le drame. Yoann me fait remarquer qu’elle a un truc bizarre sur les aigus. Plus spécifiquement, ça fait le même son sur deux notes différentes. C’est pas censé faire ça. Il me montre – effectivement le manche est un peu vrillé. Je montre ça à mon prof de guitare – il confirme, le manche est vrillé, option « merde, j’ai jamais vu ça ». Il me dit que selon toute probabilité je suis bonne pour un échange. Je retourne à la boutique, je ramène la guitare, le vendeur tente de bricoler un peu, « heuuu non là faut que ça reparte chez le fabricant, je peux rien faire. » Quinze jours plus tard, ils me rappellent, j’y retourne. Il y a effectivement eu échange standard. C’est très con, mais ça m’a fait très drôle. Pour à peu près aucune raison – elle est… identique. Mais… ben ça m’a fait drôle.

Il m’arrive de penser que j’espère que ma guitare namoi ne m’en veut pas trop de la torturer si violemment alors qu’elle aurait pu tomber dans les mains de quelqu’un qui sait jouer. Quand ça lui arrive elle fait d’ailleurs de très jolis sons 🙂 J’envisage à l’occasion de lui faire quelques infidélités et d’aller refaire un tour du côté de l’électrique. Mon petit ampli rouge me manque un peu, il fait des choses rigolotes.

Et donc, j’apprends. J’apprends pas très vite, parce que j’avoue que je travaille pas beaucoup. Le fait d’avoir un cours par semaine aide à maintenir un peu le rythme – c’est jamais agréable d’arriver et de pas y avoir touché du tout pendant la semaine. Je commence à avoir de vagues notions de solfèges (très vagues) – mes restes de collège étaient loin, et en do-ré-mi-fa-sol, alors que visiblement il n’y a qu’en France qu’on fait ça, le reste du monde est calé sur ABCDEFG. Allez comprendre. Et… je progresse. Pas vite (cf remarque précédente), mais je progresse. Je sais pertinemment que je ne serai jamais qu’une joueuse médiocre – parce que même si j’aime jouer, je sais que je ne passerai jamais les heures par jour nécessaires à devenir une joueuse potable.

Quelque part, ça a quelque chose de salutaire. J’ai eu l’énorme chance, pendant la majorité de mes études, de pouvoir plus ou moins me reposer sur le fait que je pigeais vite et bien. Ça m’a joué quelques tours (et ça m’en joue toujours). Mais je crois que je n’ai jamais aussi bien compris que « le travail, ça paye » qu’en tentant d’apprendre à jouer de la guitare. Et ça a quelque chose d’assez magique d’attraper une partition et de commencer à jouer et que ça fasse un truc qui ressemble à de la musique.

Ça fait quelque temps qu’on travaille sur Travels – un arrangement moins complexe que la version originale – et pour la première fois hier ça commençait vraiment à ressembler à quelque chose. C’est toujours assez nul, et c’est toujours pas très joli, mais ça commence à ressembler à quelque chose. Je suis aussi encore loin de jouer toutes les 5 minutes du morceau – le bout qui ressemble à quelque chose correspond aux 30 premières secondes de la vidéo YouTube 😉 Mais on avance, et mon objectif d’arriver à un truc potable sur ce truc commence à sembler abordable (c’était pas vraiment le cas il y a même trois semaines).

Il y a une semaine et demie, je me suis cassé la gueule dans un escalier en sortant de mon cours de guitare. Je sais plus exactement dans quel ordre se sont précipité les pensées suivantes : « aïe », « bon heureusement c’est pas le poignet qui a pris », et « putain ma guitare ». Il m’a fallu pas mal de temps pour avoir le courage en rentrant avant d’ouvrir le sac pour voir si elle avait pris un coup ou pas. La guitare va bien. Ma cheville commence à aller mieux.

#balisebooks – A Memory of Light – Robert Jordan et Brandon Sanderson

Publié le 27 janvier 20133 avril 2014 par Balise3 commentaires

Post original: https://plus.google.com/115810324683995775467/posts/YtbtwMxNK2e

Hier, j’ai terminé A Memory Of Light, le quatorzième et dernier tome de la série The Wheel of Time (publiée en français sous le titre La Roue du temps, ils en sont au 22e tome correspondant à la fin du 11e tome en VO) , après 3 semaines à ne guère lire que cela. J’ai pas mal râlé il y a trois semaines en voyant que la version électronique ne sortirait que dans quelques mois ; mon impatience a été plus forte que mes grommellements, et j’ai été l’acheter à la librairie. L’impatience, c’est aussi ce dont je me souviens des premiers tomes. J’avais commencé à les lire en français, mais la traduction française prenait deux tomes pour chaque tome en anglais, et l’édition de poche était bien longue à arriver après l’édition grand format… les lire en anglais était à la fois un moyen de les lire plus vite, et de faire des économies non négligeables ! (parce qu’entre un poche et deux grands formats, le choix est simple). Et tout ça, c’était… il y a un peu plus de quinze ans. Cette série m’a suivie pendant la moitié de ma vie. C’est fou.

Je suppose que ce n’est pas trop une surprise si je dis que A Memory of Light est le livre de la Dernière Bataille. Du coup, il est blindé de batailles, de combats et d’héroïsme épique. Et, de manière générale, c’est très satisfaisant. Tout le monde a son rôle, tout le monde participe au plus gros évènement jamais arrivé, et tout ça est fantastique. Je ne me serais pas attendue à apprécier autant un rapport de bataille de 900 pages – mais ça fonctionne très très bien. En tant que lecteur, on fait sa paix avec le destin de tous les personnages que l’on a suivis pendant des milliers de pages, et c’est, encore une fois, globalement satisfaisant (et quelque peu gratifiant). Certains personnages meurent, comme on peut s’y attendre dans une bataille de cette ampleur ; il n’y a pas beaucoup de temps pour les pleurer, mais on s’y attend presque aussi un peu.

Tout bien considéré, une excellente conclusion à une série qui a eu ses hauts et ses bas. Je suis très satisfaite du boulot de Brandon Sanderson – je ne sais pas s’il était « le meilleur auteur possible pour ce boulot », mais il a clairement fait un très bon boulot pour finir la série. De nos jours, je ne pense pas que je commencerais à lire une série de cette ampleur ; rétrospectivement, je suis contente que ça m’ait pris il y a 15 ans. J’aurais du mal à la recommander à quiconque – probablement de la même manière que j’aurais du mal à recommander à quiconque de courir un marathon (à commencer par moi-même 😉 ). C’est un truc gigantesque. Et quelques bouquins du milieu ne sont pas top. Est-ce que ça en valait la peine ? Je pense. C’était une chouette histoire.

Flattr

Publié le 18 janvier 2013 par Balise8 commentaires

Les plus observateurs d’entre vous auront remarqué l’apparition, depuis quelques semaines, d’un bouton vert « Flattr this » en bas des articles de ce blog (et de o< cuisine (qui est en carafe là tout de suite maintenant mais on y travaille)).

Flattr est une plateforme de micro-paiements avec un principe assez simple. Tous les mois, on dit combien on veut mettre dans la machine (il y a un montant automatique) ; pendant le mois, on peut cliquer sur les boutons Flattr ici et là qui traînent sur le web (il y en a peu, j’y reviendrai) et, à la fin du mois, le montant est redistribué équitablement aux gens chez qui on a cliqué. Flattr se « sert » au passage de 10% sur les montants distribués – l’infra c’est pas gratuit non plus. Il y a aussi un système d’abonnements pour pouvoir envoyer un Flattr tous les mois.

En fait, à la base, j’ai créé un compte Flattr parce qu’il y a « plein » de gens que j’aime bien qui ont un bouton Flattr sur leurs blogs (Matthias, Alias, Grégory, Ploum, et, depuis que je le lui ai suggéré à grands coups de pieds au cul, Delphine (qui ferait bien d’en faire autant sur son blog « principal » aussi d’ailleurs) – et si j’en oublie vous m’en voyez fort désolée (n’hésitez pas à râler dans les commentaires). Donc, j’ai créé un compte pour cliquer sur les boutons.

Et là je me suis rendue compte que mon « plein », ben en fait il était pas si « plein » que ça. Avant de créer un compte Flattr je voyais des boutons Flattr partout ; après l’avoir créé je n’en voyais plus nulle part. Ou plus exactement, « tiens, je cliquerais bien sur un bouton Flattr, dameunède, yen a pas ». Du coup, j’ai ajouté un bouton sur les miens, de blogs – parce que si ça m’agace de pas en trouver sur certains blogs, je me dis que peut-être éventuellement ça pourrait agacer de pas en trouver sur les miens. Pas que j’espère en tirer quoi que ce soit à part de quoi recliquer sur des boutons Flattr (et encore 😉 ), mais c’est peut-être aussi une manière de diffuser le truc qui, je pense, est plutôt une bonne idée.

Donc, voilà, il y a des boutons Flattr chez moi, et j’aimerais bien en trouver chez vous aussi. Juste pour avoir le plaisir de dire « tiens, c’est drôlement chouette ce que tu as pondu là, tiens, voilà un petit token de mon appréciation » 🙂

#balisebooks: Thinking, Fast and Slow (Système 1/Système 2 : Les deux vitesses de la pensée), de Daniel Kahneman

Publié le 8 janvier 2013 par Balise1 commentaire

Post original: https://plus.google.com/115810324683995775467/posts/Ssqtv5t4GC9

J’ai fini hier Thinking, Fast and Slow, de Daniel Kahneman, traduit en français sous le titre « Système 1 / Système 2 : Les deux vitesses de la pensée » (note : au moins un des avis sur Amazon signale que la traduction n’est pas terrible… peux pas juger ;)). Je l’ai acheté presque par hasard – je l’ai vu en librairie, j’ai un sourcil qui s’est levé à la mention « prix Nobel », j’ai jeté un œil à la quatrième de couverture, j’ai haussé les épaules, je me suis probablement dit « ce type ne doit pas être un pipoteur complet et il doit avoir des choses intéressantes à dire ». J’ai commencé à le lire en août, je l’ai oublié dans un coin entre temps (plus probablement, j’ai eu la flemme de le finir), je l’ai rattaqué il y a trois semaines et je l’ai enfin fini.

C’est un bouquin très intéressant, mais plutôt dense. Un sous-titre pertinent, bien qu’un peu long, pourrait être « Vous êtes nul en probas et en prise de décisions rationnelles et voici pourquoi ». Le bouquin résume à peu près 30 ans de recherche en psychologie et économie, y compris ce qui a valu à Kahneman son Nobel (en économie). Il présente deux façons de penser, ce qu’ils appellent le Système 1 et le Système 2 (d’où le titre français). Le Système 1 est rapide et intuitif (et en gros vous aide à ne pas vous faire bouffer dans la jungle), le Système 2 est plus réfléchi et logique. Et même lorsque vous pensez être entièrement rationnel et logique, il est très probable que vous ne le soyez pas (et que vous n’en soyez pas conscient). Kahneman donne beaucoup d’exemples, et explique qu’un certain nombre de facteurs influent la rationalité. Beaucoup de ces facteurs seront familiers à ceux qui ont lu You Are Not So Smart, de David McRaney; le style de McRaney est plus informel et anecdotique (c’est plus de la vulgarisation, dans le sens positif du terme); Kahneman est plutôt dans le niveau d’au-dessus, ce qui rend son bouquin un peu plus difficile d’accès (mais encore une fois très intéressant).

J’ai été surprise, amusée et déroutée par de nombreux résultats qu’il présente, et fascinée par ses explications. Je recommande chaudement.

Du vrac de #balisebooks – Takei, Colvin et Scalzi

Publié le 7 janvier 20139 novembre 2013 par Balise3 commentaires

Je suis en retard sur mes traductions de #balisebooks, donc je rattrape le retard 🙂

Oh Myyy, de George Takei

Post original: https://plus.google.com/115810324683995775467/posts/TUuYnQ8Bqxe

Un petit truc qui se lit vite: Oh Myyy, de George Takei. George Takei a joué Sulu dans Star Trek:TOS, et je dois dire que je suis assez accro à sa page Facebook, dont le contenu pourrait se résumer pour la majorité à « trucs marrants des intarwebz », avec de temps en temps des trucs plus sérieux ou de la promo personnelle – c’est plutôt un bon mélange. Et dans Oh Myyy, c’est ce dont il parle : à peu de chose près « voici comment je gère mon Facebook et ça marche plutôt pas mal ». C’est drôle et pertinent ; je n’ai pas beaucoup d’intérêt, personnellement, pour la gestion de la présence en ligne, mais j’ai trouvé son compte-rendu assez fascinant. Pas mal, quoi.

Talent is Overrated: What Really Separates World-Class Performers from Everybody Else, de Geoff Colvin

Post original : https://plus.google.com/115810324683995775467/posts/7Kt3J15gx5z

Le titre pourrait se traduire par « Le talent, c’est surfait – ce qui distingue réellement les gens qui atteignent un niveau mondial du reste du monde » (je cherche une meilleure traduction pour « performer », mais ça vient pas.) L’idée générale du livre est que les deux hypothèses « principales » qui expliquent des succès extraordinaires, à savoir un talent inné et un travail sans relâche, ne sont pas vraiment vérifiées. L’auteur développe l’idée que ce qui fait la différence est la « pratique délibérée » – un entraînement spécifiquement conçu pour améliorer sa pratique, qui peut être beaucoup répété et où un retour est immédiatement disponible. Cet entraînement est également très exigeant, et n’est pas très drôle.

Il explique comment cela s’applique à différents exemples « personnels » (des gens qui ont effectivement atteint un niveau mondial) et comment l’appliquer à une entreprise (c’était probablement la partie qui m’a le moins intéressée) et à l’éducation des enfants.

C’était plutôt intéressant à lire, ça donne de quoi réfléchir, mais le livre était peut-être un peu long/verbeux pour la quantité totale de contenu.

Redshirts, de John Scalzi

Il y a deux jours, j’étais d’humeur à lire un truc léger et marrant. Je m’étais dit que j’attendrai un peu avant de lire Redshirts, de John Scalzi, parce qu’il venait de sortir et qu’il était encore un peu cher, surtout pour une version électronique. Et bien évidemment, me dire que j’attendrai un peu était une excellente raison pour avoir envie de le lire MAINTENANT. Alors j’ai soupiré et je l’ai acheté et j’ai commencé à le lire. Et je l’ai fini hier – j’ai même poussé un peu malgré l’endormissement pour ça, ce que j’ai nettement moins tendance à faire maintenant que quand j’étais plus jeune 😉

Comme je l’ai expliqué dans un billet précédent, j’avais entendu parler de Redshirts il y a quelque temps, je priais pour que l’idée de base ne soit pas gâchée, j’ai été rassurée en lisant Le Vieil homme et la guerre, et je m’attendais à un truc chouette.

Je n’ai pas été déçue. L’idée du livre sera familière à quiconque a une vague idée de Star Trek: sur le vaisseau Intrepid, toutes les missions ont tendance à se terminer avec un troufion de base tué de façon spectaculaire. Andy Dahl, qui vient d’être assigné au vaisseau, a la ferme intention d’échapper à cette destinée et tente de comprendre ce qu’il se passe.

Redshirts contient une bonne partie des trucs qui font avoir envie de rentrer sous terre quand on regarde Star Trek (toutes séries confondues. Note : j’ADORE Star Trek), sauf peut-être la quantité de jargon technoïde – et c’est très drôle. La quantité de méta augmente exponentiellement, et l’ensemble du bouquin m’a fait ricaner plus d’une fois (comme Pierre peut probablement l’attester).

J’ai vraiment bien aimé, ça a clairement rempli les conditions « léger et marrant », et le livre est à la hauteur de ses « promesses ».

	Ja dans Y’a encore des gens sur…
	Balise dans Y’a encore des gens sur…
	Natacha dans Y’a encore des gens sur…
	Balise dans Y’a encore des gens sur…
	krysztophe dans Y’a encore des gens sur…

Flattr:

Un premier tri

Une autre méthode de tri

Flattr:

Flattr:

Flattr:

Flattr:

Flattr:

Flattr:

Flattr:

Flattr:

Oh Myyy, de George Takei

Talent is Overrated: What Really Separates World-Class Performers from Everybody Else, de Geoff Colvin

Redshirts, de John Scalzi

Flattr: