Heu, voilà, si vous lisez ce billet, c’est que vous avez trouvé où mon blog habite maintenant, bravo. (Ça veut aussi dire que j’ai pas complètement foiré mes redirections HTTP, ce qui est une bonne nouvelle). Donc, bienvenue dans les nouveaux locaux, j’espère que vous aimez la peinture, n’oubliez pas de mettre vos RSS à jour (NORMALEMENT c’est redirigé depuis l’ancienne adresse, mais je ne sais pas combien de temps ça va rester comme ça, ni même si ça marche « en pratique ») et… et voilà !
#balisebooks – Septembre 2013
Kushiel’s Scion, de Jacqueline Carey (L’Héritage de Kushiel, en français) est le premier tome de la deuxième trilogie commencée par la trilogie de Phèdre, dont j’ai causé en juin et en juillet. C’est l’histoire de l’adolescence et du passage à l’âge adulte d’Imriel, dont je ne vais pas dévoiler ici les liens avec les personnages de la première trilogie. Disons que les liens en question sont suffisants pour attirer des gens qui ne lui veulent pas que du bien, y compris quand il se décide à quitter Terre d’Ange pour aller étudier à Tiberium. Un très chouette premier tome de trilogie, avec un bon mélange d’anciens et de nouveaux personnages, et dans la lignée de la trilogie précédente (et comme j’ai bien aimé la précédente, ben j’aime bien celui-ci aussi, voilà.)
Pavilion of Women, de Pearl S. Buck (Pavillion de femmes, en français), se passe en Chine et commence juste avant la seconde guerre mondiale. La maison Wu est une des plus riches et anciennes de Chine et, le jour de ses 40 ans, Madame Wu fait part de sa décision : elle demande à son mari de prendre une seconde épouse, plus jeune qu’elle-même, et va même jusqu’à la choisir. Les conséquences de cette décision ne sont pas exactement celles qu’elle attendait, et forment la trame du livre. Et c’est fort probablement un des meilleurs livres que j’ai jamais lus, toutes catégories confondues. Bon, j’ai appris a posteriori (parce que je manque cruellement de culture) que Pearl Buck avait un Nobel de littérature, donc ya peut-être des raisons.
Little Brother, de Cory Doctorow (même titre en français), ne joue pas vraiment dans la même catégorie (même si j’ai bien aimé aussi, hein). Dans une société un peu trop salement proche de la nôtre, Marcus, un ado de 17 ans, se retrouve au mauvais endroit au mauvais moment, et est accusé de terrorisme, emprisonné et interrogé. Il finit par être relâché, et se bat alors contre la société de surveillance dans laquelle il vit. Plutôt sympathique, techniquement crédible, et même parfois didactique (parfois de façon un peu lourdingue, mais bon). Les événements courants rendent le tout d’autant plus crédible et actuel, et c’est un peu flippant. Note : la version originale de Little Brother est disponible en ligne sous licence CC-NC-SA.
Ender’s Game, d’Orson Scott Card (La Stratégie Ender, en français), est un des « classiques » de SF que je n’avais pas encore lus, voilà qui est corrigé. Ender a six ans, et il est vu comme l’ultime espoir des humains face à l’invasion imminente des aliens (qui ont déjà fait quelques dégâts historiquement). Les enfants prometteurs sont envoyés à l’école de guerre pour en faire des soldats et des officiers : l’école fournit tout un tas de jeux pour apprendre aux enfants la stratégie militaire. Ender gravit les échelons très vite, et on suit son entraînement à partir de son recrutement. C’était plutôt agréable à lire, même si on a parfois du mal à remettre ça dans le contexte de « attends, il a genre 7 ans là ? ».
Aphrodite’s Workshop for Reluctant Lovers, Marika Cobbold, était très nettement le point faible de ce mois-ci. L’idée de base était plutôt sympa – Aphrodite trouve, au vu du taux de divorce courant, que les humains ont besoin d’un coup de main pour réussir à maintenir une vie sentimentale durable – et pour qu’elle-même puisse regagner un minimum de crédibilité sur l’Olympe. La mise en œuvre est poussive, la fin prédictible et ne répond même pas au prédicat initial. Bref, c’était vraiment pas terrible.
S’il n’y en avait qu’un à lire… Pavilion of Women.
TPA : Théorème des cinq couleurs
Aujourd’hui, c’est coloriage. Je vais déjà commencer par vous montrer un petit jeu : ça s’appelle Map, c’est tout con : le jeu vous donne une carte rectangulaire avec des zones à colorier, et quelques couleurs déjà placées ; il faut colorier les autres de façon à ce que deux voisins n’aient pas la même couleur. Allez-y, allez jouer un peu avec, c’est rigolo 😛 La question théorique derrière ce petit jeu est la suivante : quel est le nombre minimal de couleurs nécessaires pour pouvoir colorier n’importe quelle carte de ce type ? Peut-être que vous vous souvenez, mais j’ai déjà un peu parlé de problèmes de ce genre là : quand j’ai parlé de P vs NP, j’ai parlé de colorabilité de graphes, et de décider si un graphe donné pouvait être colorié avec un nombre donné de couleurs. La question du nombre minimum de couleurs peut revenir à poser la question précédente plusieurs fois : « et avec 2 couleurs, ça passe ? non ? et avec trois ? non plus ? et avec quatre ? ah, cool. » Là, normalement, j’ai deux objections dans la salle. La première, c’est : « minute papillon, tu parlais de cartes et là tu me parles de graphes, c’est pas pareil, si ? ». La deuxième, c’est « heu, dis voir, demander si un graphe peut être colorié avec trois couleurs, on a vu dans le P vs NP que c’était pas trivial comme question… donc on fait quoi, surtout qu’il y a peut-être beaucoup de nombres à considérer ? ». Il se trouve que la première objection permet de répondre à la deuxième. Pour répondre à la première objection, je vais faire un petit dessin. Voilà le petit dessin.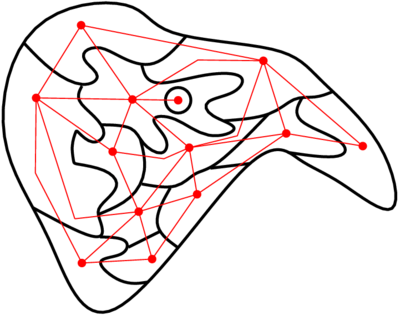 
Le petit dessin en question, il est fait comme suit :
- j’ai commencé par dessiner la carte – la structure en noir ;
- j’ai ajouté un point dans chaque zone de la carte (les points rouges) ;
- j’ai relié deux points (avec les traits rouges) si les zones correspondantes étaient voisines.
NORMALEMENT j’ai vérifié ma construction, mais si elle est bancale (si j’ai des traits en trop ou en pas assez), merci de me le signaler 🙂 Et là, que voit-on apparaître en rouge sous nos yeux ébahis ? Un graphe. Pas n’importe quel graphe, d’ailleurs : il s’agit d’un graphe planaire, c’est à dire qu’on peut le dessiner sur une feuille de papier sans que deux arcs se croisent. J’ai parlé de graphes planaires dans un billet de blog précédent : Planarité, mineurs et donuts. Là, il va falloir que vous me fassiez confiance sur quelques points. Primo, la construction ci-dessus est toujours possible. Deuzio, ça donne toujours un graphe planaire. Tertio, ce graphe planaire est unique pour une carte donnée : il a toujours le même nombre de sommets, et les arcs sont toujours les mêmes. Et c’est là qu’on répond à la deuxième objection. Oui, dans le cas général, décider si un graphe peut être colorié avec 3, 4, 5 ou 12 couleurs est difficile (au stade actuel de nos connaissances). Par contre, dans le cas particulier des graphes planaires, on sait plus de choses. Plus précisément, on connaît le théorème suivant, appelé « théorème des 4 couleurs » :
Tout graphe planaire peut être colorié avec au maximum 4 couleurs.
Et, comme corollaire au point précédent, je peux colorier une carte avec quatre couleurs (il suffit de faire ma petite construction là-haut, de colorier le graphe résultant, et de colorier chaque zone avec la couleur du sommet en question – rappelons que dans le cas qui nous intéresse, un coloriage est valide si deux sommets reliés par un arc n’ont pas la même couleur.) Un petit aparté: je parle de « cartes » ici, mais c’est pas vraiment applicable directement « dans la vraie vie ». Le problème principal, c’est que certains pays ne sont pas « connectés ». Et si on colorie une carte du monde, on s’attend à ce que, par exemple, la Guyane soit de la même couleur que la France. Ce qui ajoute des arcs entre la zone « France » et les zones « Brésil » et « Suriname », et qui risque fort de nuire à la planarité du graphe correspondant. Fin de l’aparté, revenons à nos moutons. Donc, si j’ai un graphe planaire, je peux répondre directement à la question « est-ce que ce graphe peut être colorié avec k couleurs » par « oui », dès que k est supérieur ou égal à 4. La preuve du théorème des quatre couleurs est… compliquée. J’en parlerai dans un prochain billet, mais il faut que je me documente encore un peu avant sur le sujet 🙂
Un résultat intéressant est que pour trois couleurs, même dans le cas « graphe planaire », le problème reste NP-complet ! (C’est un résultat de Stockmeyer en 1973, dans un article intitulé « Planar 3-colorability is polynomial complete », qui 40 ans plus tard est toujours planqué en tant qu’article payant à l’ACM. Mais je digresse.) Donc, pour 3 couleurs, c’est dur à décider, pour 4 couleurs, on sait qu’on peut le faire, mais c’est dur à prouver. En revanche, le théorème suivant est relativement simple à prouver :
Tout graphe planaire peut être colorié avec au maximum 5 couleurs.
J’ai dit que c’était relativement simple à prouver, et donc je vais le faire. Ça va quand même être probablement un peu long, donc accrochez-vous, et je vais essayer de faire preuve de pédagogie 🙂
J’ai besoin d’un premier résultat pour ma preuve :
Tout graphe planaire contient au moins un sommet de degré au plus 5.
Le degré d’un sommet, c’est le nombre d’arcs qui y sont connectés. Comme un arc connecte exactement deux sommets, si je fais la somme des degrés de tous les sommets, j’obtiens deux fois le nombre d’arcs (parce qu’un arc donné est compté exactement deux fois, une fois à chacune de ses extrémités). Maintenant, je vais vous demander d’admettre encore un truc, c’est qu’on connaît le nombre maximal d’arcs d’un graphe planaire, en fonction de son nombre de sommets, n : il y a au plus 3n-6 arcs, dès qu’il y a plus de deux sommets (comme on me l’a fait remarquer en commentaire). Je pourrais aussi le démontrer, mais ça implique encore un résultat intermédiaire, et ce billet va finir par être vraiment beaucoup trop long (dit-elle au bout de deux pages). Comme j’ai au plus 3n-6 arcs, la somme des degrés de tous les arcs d’un graphe planaire est inférieure ou égale à 6n-12. Par conséquent, il y a au moins un sommet de degré au plus 5 : si ce n’est pas le cas, la somme des degrés de tous les arcs est supérieure ou égale à 6n (6 arcs, multipliés par n sommets), et ce n’est pas possible pour un graphe planaire.
Revenons à nos moutons initiaux : on veut maintenant démontrer que tout graphe planaire peut être colorié avec au maximum 5 couleurs. On va faire un raisonnement par récurrence sur le nombre de sommets du graphe. J’ai interrompu la rédaction de ce billet pour aller faire un billet sur le raisonnement par récurrence, allez le lire si le terme ne vous est pas ou plus clair 🙂 Donc, on commence par traiter l’hypothèse de base. Si mon graphe n’a qu’un seul sommet, je peux le colorier avec au maximum 5 couleurs : j’en choisis une pour mon sommet, et voilà.
Maintenant, je suppose que l’hypothèse de récurrence suivante est vraie : tout graphe planaire à (n-1) sommets peut être colorié avec au maximum 5 couleurs. Le but du jeu est maintenant de déduire, à partir de ça, que tout graphe planaire à n sommets peut être colorié avec au maximum 5 couleurs. Pour ça, on considère un graphe à n sommets, n’importe lequel (si je démontre que ça marche pour n’importe quel graphe, je montre que ça marche pour tous les graphes). Par le résultat intermédiaire que j’ai prouvé au-dessus, le graphe à n sommets étant planaire, il a un sommet de degré inférieur ou égal à 5, qu’on va appeler v dans la suite pour aller vite. On peut prendre v, et le retirer temporairement (on retire aussi tous les arcs qui y sont connectés). Le graphe sans v est un graphe planaire à (n-1) sommets. Donc, on peut le colorier avec au maximum 5 couleurs. Maintenant, on remet v (et les arcs qu’on a retirés aussi) : on obtient un graphe à n sommets dont (n-1) sommets sont coloriés avec au maximum 5 couleurs, et un sommet, v, n’a pas encore de couleur.
Là, on a deux possibilités. Si les voisins de v (les sommets auxquels v est connecté) utilisent moins de 5 couleurs, on peut utiliser une des couleurs non utilisées pour colorier v, et le graphe initial est colorié avec au maximum cinq couleurs.
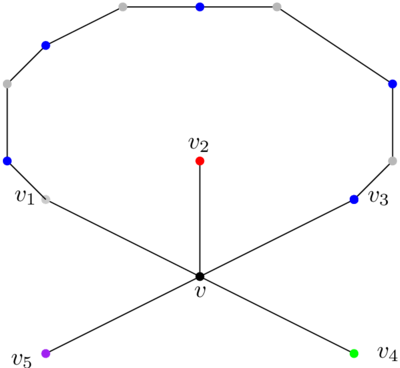
Sinon, si on prend une représentation plane du graphe planaire, on est dans la situation suivante :
Je n’ai dessiné ici que six sommets, v et ses cinq voisins. Le graphe peut contenir plus de sommets et plus d’arcs, mais il contient forcément cette structure.
Sur ma représentation plane, je choisis arbitrairement un voisin de v, je l’appelle v1, et je numérote les autres dans le sens des aiguilles d’une montre (v2 à v5). Les sommets v1 à v5 sont de cinq couleurs différentes. Je vais maintenant prouver que je peux soit colorier v1 et v3 de la même couleur, soit colorier v2 et v4 de la même couleur.
Je regarde d’abord v1 et v3, et plus précisément je m’intéresse au sous-graphe colorié avec les couleurs de v1 et de v3, c’est-à-dire que je prends tous les sommets de la couleur de v1 (gris, sur la figure) et tous les sommets de la couleur de v3 (bleu, sur la figure), et tous les arcs du graphe initial qui relient ces sommets entre eux. Un exemple sur un petit graphe :
À droite, j’ai représenté le sous-graphe du graphe de gauche en ne prenant que les sommets bleus et gris (j’ai supprimé les sommets rouges et violets, et les arcs qui y étaient attachés). Sur ma figure, j’ai quatre sommets entre lesquels j’ai des chemins (une suite d’arcs qui me permettent de passer de l’un à l’autre), et un sommet qui n’a de chemin vers aucun autre.
Si je ne regarde que les sous-graphe bleu/gris de mon graphe initial, j’ai deux possibilités : soit v1 et v3 ne sont plus connectés, soit ils le sont encore ; et par « connectés », j’entends qu’il y a un chemin entre v1 et v3. S’il n’y a pas de chemin, v1 et v3 sont dans des composants différents (un composant, c’est un ensemble de sommets qui sont reliés les uns aux autres par des chemins). Dans ce cas là, je regarde le composant qui contient v3 (il se peut que ce soit v3 tout seul, mais sinon c’est un ensemble de sommets bleus et gris qui ont tous un chemin connecté à v3). Dans ce composant-là, le fait que les sommets soient bleus ou gris est arbitraire : je peux inverser les deux couleurs sans que ça ait un impact sur le fait que le graphe est correctement colorié. Si je ne fais ça que dans ce composant là, v1 (qui n’est pas dans composant en question) reste gris, et v3 (qui était bleu) devient gris. Maintenant, je peux remettre le « reste » du graphe (les sommets rouges, violets, verts, et le sommet v qui n’est pas encore colorié) : comme je n’ajoute pas de sommets bleus ou gris, le coloriage reste valide. Et j’ai « libéré » le bleu pour mon sommet v : donc, je peux colorier v en bleu. La vie est belle.
Enfin, presque. Parce qu’il se peut aussi que v1 et v3 soient dans le même composant « bleu/gris ». Donc là, si j’inverse le bleu et le gris, ben je me retrouve avec v1 en bleu, et v3 en gris, et je peux toujours rien faire avec v. Donc, il faut trouver une autre astuce.
Je regarde maintenant le sous-graphe composé des sommets coloriés avec les couleurs de v2 (rouge) et v4 (vert) : je retire tout ce qui n’est pas rouge ou vert du graphe, et je regarde ce qui reste. Si v2 et v4 ne sont pas dans le même composant rouge/vert, je peux inverser le rouge et le vert dans le composant de v4. v2 reste rouge, v4 devient rouge, et je peux colorier v en vert. Là, j’ai peut-être quelqu’un qui me dit « oui, mais si v2 et v4 sont aussi dans le même composant, tu as le même raisonnement et donc le même problème que pour le composant bleu/gris ! ». Oui, mais. Regardons un peu ce qui se passe sur la figure. Comme v1 et v3 sont dans le même composant bleu/gris (sinon, on n’aurait pas besoin de regarder ce qui se passe dans le composant rouge/vert), il y a un chemin entre v1 et v3 composé de sommets bleus et gris.
Si je veux faire un chemin composé de sommets verts et rouges entre v2 et v4 (ce qui est la condition pour que v2 et v4 soient dans le même composant rouge/vert), ça bloque : soit je dois croiser l’arc entre v et v3, soit je dois croiser un des arcs du chemin bleu/gris entre v1 et v3. Et comme mon graphe est plan… ben j’ai pas de croisement entre mes arcs. Donc, v2 et v4 ne peuvent pas être dans le même composant, donc je peux bien inverser les couleurs du composant de v4, et colorier v en vert.
J’ai donc regardé tous les cas possibles pour mon graphe, et dans tous les cas, je peux colorier le sommet v de façon valide. Donc, si un graphe avec (n-1) sommets peut être colorié avec au maximum 5 couleurs, alors un graphe avec n sommets peut être colorié avec au maximum 5 couleurs, ce qui termine mon étape de récurrence et donc la preuve du théorème des cinq couleurs. Ouf.
J’avais initialement prévu de parler du théorème des 4 couleurs plus en détail dans ce billet, mais je crois que je vais arrêter là pour ne pas fumer plus de neurones de mon lectorat (en espérant qu’il y en ait quand même une partie qui soit arrivée jusqu’ici…). Comme d’habitude, pour les questions, typos, remarques, etc., c’est dans les commentaires que ça se passe 🙂
Raisonnement par récurrence et raisonnement par l’absurde
Pouf pouf, un petit billet vite fait pour pouvoir y faire référence plus tard – je suis en train de faire un autre monstro-billet, et je me suis rendue compte que j’avais besoin des éléments suivants pour faire un truc qui tienne à peu près debout, donc hop, un deuxième billet ! Je vais causer ici de deux outils fondamentaux dans la « boîte à outils » nécessaire pour prouver des trucs : le raisonnement par récurrence et le raisonnement par l’absurde. Ce sont des outils qui sont présentés et utilisés au moins au lycée (du moins de mon temps 😉 ), et qu’on retrouve à longueur de temps, partout, donc autant expliquer comment ça marche.
Le raisonnement par récurrence
Le principe du raisonnement par récurrence, c’est les dominos. Pas ceux avec des points, ceux qu’on fait tomber. On sait que si on fait tomber un domino, le suivant tombe aussi. Et on fait tomber le premier domino. Du coup, tous les dominos tombent.
Pour le raisonnement par récurrence, c’est pareil. On a une propriété qui dépend d’un entier, et on veut prouver qu’elle est vraie pour n’importe quel entier. Donc ce qu’on fait, c’est qu’on commence par montrer qu’elle est vraie pour un petit entier, genre 0, 1, 2 (parfois les cas pour 0 ou 1 n’ont pas beaucoup de sens). Et on montre que si elle est vraie pour un entier k, alors elle est vraie aussi pour un entier k+1. Du coup, on a le « départ » des dominos (« c’est vrai pour 0 ») et le « chaînage » des dominos (« si c’est vrai pour n, c’est vrai pour n+1 ») ; et si ces deux conditions là sont vraies, alors tous les dominos se cassent la gueule (« la propriété est vraie pour tous les entiers à partir de celui qu’on utilise comme cas de base »).
Là, je suis un peu embêtée, parce que j’ai un exemple qui marche, mais la preuve est assez nulle par rapport à une autre, qui est plus jolie. Donc je vais montrer les deux 🙂 Je veux démontrer que la somme des entiers de 1 à n est égale à n(n+1)/2, pour n’importe quel n. Je commence par n = 1 : j’ai bien 1(1+1)/2 = 2/2 = 1, donc l’hypothèse de base est vraie.
Ensuite, je suppose que c’est vrai pour un entier k, c’est à dire que la somme des entiers de 1 à k est égale à k(k+1)/2. Maintenant, je calcule la somme des entiers de 1 à k+1 : 1 + 2 + 3 + … + (k-1) + k + (k+1), c’est égal à la somme des entiers de 1 à k, plus (k+1). Par hypothèse de récurrence, c’est égal à k(k+1)/2 + k+1 = (k² + k + 2k + 2)/2 = (k² + 3k + 2)/2. Pour que ma preuve fonctionne, je veux que la somme des entiers de 1 à k+1 soit égale à (k+1)(k+2)/2. Et il se trouve que (k+1)(k+2), ça fait précisément k² + 3k + 2.
J’ai donc mon hypothèse de base, mon étape de récurrence, et j’ai prouvé ce que je voulais prouver.
Pour le fun, la preuve que je préfère sur cette égalité, c’est celle-ci : on considère un tableau à deux lignes et n colonnes :
1 2 3 4 ... n-2 n-1 n n n-1 n-2 n-3 3 2 1
et on additionne les deux lignes. Chaque colonne vaut n+1 : c’est le cas pour la première colonne, et à chaque étape, on ajoute 1 à la première ligne et on enlève 1 à la deuxième ligne, donc la somme reste identique. (Quelque part, ici, je fais du raisonnement par récurrence sans vraiment le dire !). J’ai n colonnes, donc si j’additionne tous ces résultats, ça fait n(n+1). Et si je fais la somme dans l’autre sens, la première ligne est égale à la somme des entiers de 1 à n, la deuxième ligne aussi… donc mon n(n+1), c’est aussi deux fois la somme des entiers de 1 à n.
Le raisonnement par l’absurde
Le raisonnement par l’absurde est parfois un peu dangereux/délicat, parce qu’il est parfois utilisé à tort et à travers. Admettons que je veuille prouver qu’une phrase A est vraie. L’idée du raisonnement par l’absurde, c’est de partir du principe que A est faux, de dérouler une suite d’arguments impliqués par le fait que A est faux, et d’arriver à quelque chose qu’on sait être impossible. Si le fait que A est faux implique que quelque chose d’impossible arrive, c’est que A est vrai, sinon l’univers se casse la gueule et ça fait désordre.
Mon exemple préféré, c’est de démontrer que 
J’ai besoin d’une toute petite preuve au passage : j’affirme que si un entier n est pair, alors son carré n² est pair, et que si n² est pair, alors n est pair. Si n est pair, je peux l’écrire comme n = 2k, et donc n² = 4k² = 2 × 2k², donc n² est pair. Si n est impair, je peux l’écrire comme n = 2k+1, donc n² = 4k² + 2k + 1 = 2(2k² + k) + 1, donc n² est impair. Donc si n² est pair, il ne peut pas arriver que n soit impair (parce que sinon n² serait impair aussi), donc n est pair.
Donc, supposons qu’on puisse écrire 
#balisebooks – Août 2013
Tiens, je suis en retard pour mon #balisebooks. Étonnant, non ? Non. Sans plus attendre, donc…
The Ghost Brigades, de John Scalzi (en français Les Brigades fantômes) – deuxième tome qui se passe dans l’univers du Vieil homme et la guerre (Old Man’s War), dont je parle dans un autre #balisebooks. Entre temps, Scalzi a gagné le Hugo pour Redshirts – j’ai donc eu le plaisir hipster d’avoir lu le Hugo avant qu’il soit attribué, ça, c’est fait. Bref, Ghost Brigades. Je l’ai trouvé nettement en deçà de Old Man’s War, ça, c’est un fait. On suit l’histoire de Jared Dirac, qui fait partie desdites brigades fantômes – une force spéciale de l’armée composée de gens-qui-sont-morts-dont-on-a-récupéré-l’ADN-pour-faire-des-supersoldats. Et là-dessus, la guerre approche, et Dirac se retrouve (complètement pas par hasard) à être le dernier espoir de l’éviter. Les brigades fantômes faisaient clairement partie des choses laissées en suspens dans Old Man’s War ; Ghost Brigades vise au moins en partie à expliquer tout ça. Et c’est plutôt bien fait, c’est crédible (dans l’univers en question), c’est bien écrit, tout ça – mais ça reste décevant par rapport à Old Man’s War. Évidemment, c’est peut-être injuste de comparer les deux - peut-être que sans le premier, j’aurais trouvé le deuxième plus chouette, allez savoir. Dans tous les cas, ça reste une lecture agréable, hein - mais vaguement décevante.
Biting Bad, de Chloe Neill (pas encore de titre français) - huitième tome de Chicagoland, qui est possiblement ma série de littérature-à-vampires préférée et dont, apparemment sauf erreur de ma part, je n’ai pas encore parlé dans #balisebooks (ils ont dû tomber dans le trou noir sans #balisebooks). La série Chicagoland se passe, de façon hyper prévisible, à Chicago. Merit, l’héroïne, est transformée en vampire à l’insu de son plein gré dans le premier tome, et est enrôlée au sein de la maison Cadogan, une des trois maisons de vampires établies à Chicago. Elle devient Sentinelle de ladite maison, et dans la grande tradition de série de littérature-à-vampires, se tatane l’ennemi-de-l’année-du-tome dans chaque tome. J’aime particulièrement cette série-là parce que je trouve les personnages vraiment sympa ; j’aime aussi le fait que les vampires, ben ils mangent (de la « vraie » nourriture), et qu’ils ont l’air de bien bouffer. C’est aussi une série qui me fait dire que j’irais bien à Chicago, à l’occasion (en partie pour la raison sus-citée, il faut l’admettre.) Dans ce huitième tome, que j’avais précommandé et que j’ai lu dans la semaine suivant sa publication, une série d’émeutes anti-vampires secoue Chicago. Qui se cache derrière et comment les arrêter ? Et c’est un bon tome de la série - c’est plutôt bon signe, je trouve, si le huitième tome reste à un bon niveau. Vivement le neuvième ! (Février 2014… bon 🙂 )
The Perks of Being a Wallflower, de Stephen Chbosky (Le Monde de Charlie, en français), est l’histoire de Charlie, un lycéen un peu bizarre, timide, introverti, et tout ce qui s’en suit. Le livre est composé de « lettres » de Charlie à un lecteur non nommé. C’est assez bizarre, comme bouquin, parce que l’histoire en soi est assez peu crédible (Charlie a une quinzaine d’années mais on a parfois l’impression qu’il en a huit), mais les détails de l’histoire sont plutôt chouettes. Globalement, j’ai bien aimé, mais je suis pas exactement sûre de savoir pourquoi.
Death’s Daughter, d’Amber Benson (pas traduit à ma connaissance) est un bouquin que j’ai acheté à cause de son auteur, qui joue Tara dans Buffy. Il raconte l’histoire de Calliope Reaper-Jones qui, on l’apprend assez vite et on le devine dans le titre, se trouve être la fille de la Mort (Death, en anglais). Le truc gênant, c’est que Death (le papa de Calliope, donc) s’est fait enlever, et que Calliope hérite par conséquent de l’entreprise familiale le temps que tout revienne à sa place. Calliope n’ayant aucune envie de se retrouver dans cette situation, elle se met à la recherche de son père (et de sa sœur qui a eu le mauvais goût de se faire enlever en même temps). Verdict : ça se lit, mais c’est pas grand. J’ai pas détesté, mais bon, vite lu vite oublié, je pense.
Queen Unseen: My Life with the Greatest Rock Band of the 20th Century, de Peter Hince, est exactement ce que le titre dit 😉 J’ai trouvé ça par hasard sous un petit pois en promo sur Amazon l’autre jour, me suis dit « boah pourquoi pas », et donc j’ai lu ça en août. Peter Hince a été « roadie » (la wikipédia me suggère « machiniste itinérant » comme traduction, admettons - bref, un mec qui bosse sur les tournées, quoi) de Queen pendant des années, et c’est son autobiographie. Plutôt sympa d’avoir une idée de ce à quoi peuvent ressembler les coulisses d’un machin pareil – un peu bordélique, comme bouquin, mais finalement assez drôle.
Voilà, c’est tout pour le mois d’août !
S’il n’y en avait qu’un à lire… Biting Bad.
TPA – Planarité, mineurs et donuts
Pour le premier Théorème à Périodicité Aléatoire, on va parler de graphes, et on va faire des petits dessins. Un graphe est un ensemble de sommets reliés entre eux par des arcs. Pour décrire un graphe, je peux par exemple dire « il a les sommets 1, 2, 3, 4 et 5, et des arcs entre les sommets 1 et 2, 2 et 3, 3 et 4, 4 et 1, 1 et 3, 2 et 4, 1 et 5, et 4 et 5 ». Je peux aussi décider de le dessiner sur une feuille de papier, et je peux dessiner ça de plusieurs manières : tous les dessins, là, sont une représentation de ce graphe.
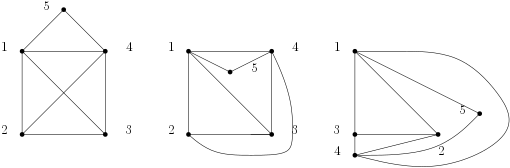
Dans ces trois représentations, deux sont dites planes : le graphe est dessiné de façon à ce que les arcs du graphe ne se croisent pas. La première représentation n’est pas plane : les arcs 1-3 et 2-4 se croisent. Un graphe qui peut être dessiné dans le plan (c’est-à-dire sur une feuille de papier plate) sans que deux arcs se croisent est un graphe planaire. Le fait qu’on ait un adjectif pour ça devrait vous faire dire qu’il existe des graphes non planaires, c’est-à-dire qu’on ne peut pas dessiner dans le plan sans croiser deux arcs. Deux exemples classiques (et utiles pour la suite) de ce type de graphes sont le graphe complet sur 5 sommets (je prends 5 sommets et j’ajoute tous les arcs possibles), qu’on appelle en abrégé 
Et le théorème suivant, dû à Wagner en 1937, dit que si un graphe n’est pas planaire, c’est parce que, quelque part dans sa structure, on trouve un truc qui ressemble à
Un graphe est planaire si et seulement s’il ne contient le mineur
Je triche un peu, parce que je n’ai pas encore défini la notion de mineur. Donc, définissons :
Un mineur d’un graphe G est un graphe obtenu à partir de G en effectuant zéro ou plusieurs suppression d’arc, suppression de sommet ou contraction d’arc.
Supprimer un arc, c’est facile : si deux points sont reliés par un arc, on peut décider qu’en fait non, et supprimer l’arc. Supprimer un sommet, c’est facile aussi : on choisit un sommet, on le supprime, et on supprime aussi tous les arcs qui y sont reliés, parce que sinon on sait pas où ils vont de toute façon. La notion de contraction est un tout petit peu plus sioux. L’idée, c’est qu’on prend deux sommets reliés par un arc, et qu’on les transforme en un seul sommet. Le sommet résultant est attaché à tous les arcs qui étaient dans le graphe précédent. On peut imaginer qu’on « pince » deux sommets qui se rapprochent, qui se rapprochent, qui se rapprochent et POUF qui n’en font plus qu’un. Un petit exemple, dans lequel je contracte l’arc rouge et dans lequel j’obtiens le sommet rouge :
Donc, en gros, ce que Wagner dit, c’est que « si je bricole mon graphe un peu et que j’arrive à faire apparaître
Il se trouve qu’il existe un théorème qui généralise cette idée de « mineurs exclus » – c’est un théorème de Robertson et Seymour dont la preuve prend… 20 articles, publiés de 1983 à 2004. Le théorème s’énonce comme suit :
Toute famille de graphe fermée pour les mineurs peut être décrite par un ensemble fini de mineurs exclus.
Explications : une famille de graphes fermée pour les mineurs, c’est un ensemble de graphes tels que, si je prends un graphe quelconque de cet ensemble, que j’en prends un mineur (avec la définition précédemment donnée), alors le mineur est aussi dans la famille en question. Ce que Robertson et Seymour disent, c’est que dans une famille comme ça, il existe un ensemble fini de mineurs exclus, c’est-à-dire que si on trouve ce mineur dans un graphe, alors le graphe ne fait pas partie de la famille.
Appliquons ça à l’exemple des graphes planaires. Les graphes planaires sont une famille de graphes fermée pour les mineurs : si je prends un mineur d’un graphe planaire, je peux toujours dessiner le mineur en question dans le plan sans avoir de croisement d’arc. Et les mineurs exclus sont
Là où ça devient drôle, c’est qu’en général, on ne connaît pas les mineurs exclus en question. On sait qu’ils existe, on sait qu’il y en a un nombre fini, mais on ne sait pas quelle tête ils ont. Un petit exemple pour terminer : supposons que je veuille dessiner mon graphe non pas sur une feuille de papier, mais sur un tore – un donut, si ça vous parle plus.
L’idée, ça serait que je dessine des points sur mon donut, et que je les relie avec des arcs, exactement comme je le fais dans le plan. Si je fais ça, et que j’arrive à dessiner mon graphe sans croiser d’arcs, j’ai un graphe non pas planaire, mais toroïdal (ou donutidal, si vous voulez). La famille des graphes toroïdaux est fermée pour les mineurs, donc il existe une famille de mineurs exclus pour cette famille. Jusqu’à présent, on en a trouvé plus de 16 000. Et on ne sait pas combien il y en a au total. Amusant, non ?
(Et si vous voulez essayer de tous les trouver, je crois qu’il faut commencer par faire des donuts 😉 )
Introduction : Théorème à périodicité aléatoire – TPA
Hoplà,
J’ai toujours dans l’idée de faire un billet ou deux ou 12 sur les algos aléatoires, mais comme c’est long et que j’ai pas encore décidé par où attaquer, je vais faire d’autres trucs en attendant, parce que bon, ya pas de raison.
J’introduis donc aujourd’hui une série de Théorèmes à Périodicité Aléatoire, ou TPA – des billets que je vais essayer de faire courts, mais à dates aléatoires (je tiens pas à faire « le théorème de la semaine », ça risque de durer 3 semaines et encore…), présentant un résultat rigolo, éventuellement des éléments de preuve si elle tient dans la contrainte « billet court », probablement majoritairement dans le domaine informatique théorique / combinatoire, mais sait-on jamais, je vais peut-être me retrouver à diverger à un moment…
Ceci est un billet d’annonce – un vrai billet avec un vrai théorème devrait apparaître ici cet après-midi ou demain. Spoiler : ça va parler de graphes.
#balisebooks – Juillet 2013
Je disais donc que j’allais faire les bouquins de juillet dans les heures ou jours qui suivraient le 1er août ; il semblerait que la semaine soit passée sans que je m’en rende compte. Faut dire aussi, on a récupéré notre appartement et on a remménagé, entre temps. Alors, bon.
Pas tant de livres que ça lus en juillet – probablement la « faute » aux deux tomes de la Phèdre’s Trilogy qui sont tout de même assez volumineux (plus de 650 pages chacun…)! Comme précédemment, dans l’ordre de lecture.
Kushiel’s Chosen, de Jacqueline Carey (en français L’Élue) – deuxième tome de la trilogie de Phèdre dont j’ai parlé pour le #balisebooks de juin. Ce tome se passe dix ans après le premier tome ; Phèdre est établie dans une propriété choupi et tout se passe bien. Jusqu’à ce qu’un certain colis arrive – et Phèdre doit repartir à l’aventure. En jeu : le trône de Terre d’Ange, rien que ça. Peut-être un peu en deçà du premier tome, mais très chouette néanmoins, et une bonne transition entre le tome 1 et le tome 3.
Kushiel’s Avatar, de Jacqueline Carey (en français L’Avatar) – troisième tome de la même trilogie, est à mon avis le meilleur des trois. Phèdre cherche à libérer un ami d’un destin peu enviable, et se retrouve pour se faire à aller sauver un gamin kidnappé par une espèce de secte maléfique. C’est aussi le tome le plus violent – et peut-être le plus marquant, pas forcément dans le bon sens du terme : il faut parfois avoir le cœur bien accroché. Et je n’arrive pas à décider si c’était un excellent bouquin à cause ou en dépit de ça. Mais, en tous cas, une trilogie phénoménale, recommandée. Pour la petite histoire, d’ailleurs, j’ai appris l’existence de cette trilogie en regardant une vidéo de Geek&Sundry, la chaîne YouTube gérée entre autres par Felicia Day ; Geek&Sundry avait une série intitulée The Story Board, qui était en gros une série de panels d’auteurs sur différents sujets, et c’était très chouette. Et, donc, Jacqueline Carey était dans un épisode de cette série, et c’est comme ça que j’ai découvert ça.
SuperFreakonomics, de Steven Levitt et Stephen Dubner (même titre en français) – autant j’avais bien aimé Freakonomics, qui avait tout un tas d’anecdotes et de corrélations amusantes, autant ce deuxième essai est à mon avis raté. Ça part bien, et à peu près à la moitié du bouquin ils se mettent à causer climat, et ça part dans le n’importe quoi chiant. J’ai pô aimé.
Spin, de Robert Charles Wilson (même titre en français) – un excellent bouquin de SF. J’ai trouvé ça dans le Humble Bundle eBooks 2 (qui est depuis terminé) ; c’est pas COMPLÈTEMENT IMPOSSIBLE que j’en aie une version papier dans ma bibliothèque (actuellement encore en cartons) que j’avais pas encore lue (ça me dit confusément quelque chose…), mais, bref. L’idée de Spin est la suivante : un beau jour (ou plutôt une belle nuit), toutes les étoiles s’éteignent. Et il est expliqué assez vite que la Terre est en fait enveloppée dans une membrane plus ou moins étanche, avec en plus la propriété amusante de ralentir le temps à l’intérieur. Du coup, la durée de vie du Soleil (et son explosion) devient un problème vachement plus urgent, parce que quand il se passe un an sur Terre, il s’en passe 100 millions dehors. Gênant. La fin est un peu décevante, mais j’ai adoré le bouquin. J’ai vu récemment qu’il s’agissait en fait d’une série : je vais penser sérieusement à me procurer les tomes suivants.
La Petite garce dans la prairie, d’Alison Arngrim (en anglais Confessions of a Prairie Bitch) – l’autobiographie de « Nellie Oleson de la Petite maison dans la prairie », que j’ai achetée principalement parce que c’était une offre Kindle Éclair. Pas mal d’anecdotes de tournage et de « autour » (elle raconte à un moment qu’elle est allée aux Enfants de la télé en France, et qu’elle a halluciné d’entendre le public CHANTER LE GÉNÉRIQUE… instrumental !), mais pas seulement. Certains passages vraiment pas marrants, mais… c’est la vie 
mais en-dehors de ça, j’ai vraiment beaucoup ri. Et comme une envie de regarder la Petite maison dans la prairie 🙂
S’il n’y en avait qu’un à lire… Spin.
#balisebooks – Juin 2013
Il se trouve que, apparemment, parler de ce que je lis au fur et à mesure, ça marche pas top. Comme on est le premier août, je tente une nouvelle formule, qui est de causer le premier (ou le 5) du mois des bouquins que j’ai finis dans le mois précédent – information à laquelle j’ai accès grâce à mon GoodReads préféré. (Sérieusement, GoodReads, c’est bien.) Et comme j’ai, en juillet, des bouquins d’une trilogie que j’ai commencée en juin, ben je commence par juin, voilà. Voici, donc, par ordre de lecture, ce que j’ai fini de lire en juin. Et du coup, je fais la VF ici d’abord, et je ferai la traduction sur G+ plus tard.
Tears in Rain, de Rosa Montero (Des Larmes sous la pluie, en français) – un thriller très sympa, dans un univers très largement inspiré de Blade Runner. L’héroïne, Bruna, est une réplicante, consciente de l’être et d’avoir une durée de vie très limitée. Elle enquête sur une série d’événements : un réplicant tue un autre réplicant puis se suicide. Pas le truc le plus mémorable du monde, mais un bon moment. J’avais récupéré ça sur l’offre éclair Kindle, pas regretté.
Food rules, de Michael Pollan (Les règles d’une saine alimentation, en français) – Pollan fait partie de ces gens dont on cause pas mal en ce moment, je me suis dit « tiens je vais en lire un », mais j’ai visiblement pas choisi le bon. Une « règle » par page, un paragraphe par règle – bon. Ça m’apprendra à ne pas faire attention à ce que je fous sur mon app Kindle. Pis bon, je croyais que le « rules » du titre était un verbe et pas un nom, ça aurait été mieux, sans doute 🙂
Une Autobiographie transsexuelle (avec des vampires), de Lizzie Crowdagger – ça, je sais plus comment je suis tombée sur ce blog, j’ai lu des extraits qui m’ont beaucoup fait rire, du coup j’ai acheté le bouquin (qui est en gros ce que son titre dit – en trois grosses nouvelles), j’ai bien rigolé, une chouette découverte. Pareil, pas super mémorable, mais sur le coup, sympa.
Le Jeu de l’ange, de Carlos Ruiz Zafón – j’avais vraiment beaucoup aimé L’Ombre du vent, j’ai nettement moins aimé celui-ci. C’est plus ou moins la suite de l’Ombre du vent, et c’est l’histoire de David Martin, qui rêve d’avoir du succès en tant qu’écrivain. C’est un peu pénible, parce que j’ai adoré la première moitié du bouquin, et j’ai vraiment pas accroché sur la deuxième moitié du bouquin qui est partie dans le bizarre à la fois peu crédible et peu passionnant.
Ready Player One, d’Ernest Cline (Player One, en français) est un machin complètement jubilatoire. C’est l’histoire d’un gamin qui vit dans un univers vaguement futuriste où les habitants passent la majeure partie de leur temps dans OASIS, un genre de Second Life avec une interface de réalité virtuelle. Le créateur d’OASIS, James Halliday, est mort, et à sa mort, une chasse au trésor géante et difficile a commencé. À la clé : l’héritage dudit James Halliday. Et James Halliday, le truc qui le faisait triper, c’était les années 1980. Du coup, c’est un prétexte pour un voyage dans la culture geek des années 80, c’est bien fichu, c’est très drôle, et j’ai beaucoup aimé. Bon, je suis clairement en plein dans le public cible aussi 😉
Kushiel’s Dart, de Jacqueline Carey (La Marque, en français) est le premier tome de la trilogie de Phèdre, une série de fantasy qui se passe dans une espèce d’Europe parallèle à peu près au niveau Renaissance. Phèdre est une courtisane, qui se retrouve a/ choisie par les dieux/anges pour tirer du plaisir dans la douleur b/ et par conséquent adoptée par son mentor, Anafiel Delaunay, qui la forme comme espionne de haut niveau. Et, évidemment, ça part en sucette assez rapidement, le jeu des intrigues politiques étant ce qu’il est. La particularité de Phèdre rend l’histoire parfois un peu dérangeante (certaines scènes sont difficiles, il faut le dire, et pas à laisser aux mains des enfants), mais globalement c’est un excellent bouquin. Je lis assez peu de fantasy, mais si Jacqueline Carey continue à en écrire je continuerai probablement à en lire (j’ai un peu de retard !).
Let’s Pretend This Never Happened, de Jenny Lawson (pas de traduction française) est une série de chroniques autobiographiques plus ou moins exagérées (je me demande dans quelle mesure) par Jenny Lawson, a.k.a. The Bloggess. Et The Bloggess, ben elle me fait beaucoup rire. Et son bouquin, il m’a beaucoup fait rire aussi. C’est du grand n’importe quoi en barres, avec des animaux empaillés dedans.
The Murder of Roger Ackroyd, d’Agatha Christie (Le Meurtre de Roger Ackroyd) est un grand classique que j’avais déjà lu, probablement plusieurs fois, quand j’étais gamine (j’ai lu beaucoup d’Agatha Christie), mais que j’ai redécouvert avec grand plaisir. C’est un Agatha Christie, que dire de plus. Celui-là est particulièrement chouette.
Voilà, c’est tout pour juin, je ferai juillet dans la journée/les jours qui viennent.
S’il n’y en avait qu’un à lire… Kushiel’s Dart.
Je sers la science et c’est ma joie
J’ai récemment participé, en tant que « volontaire », à une étude scientifique à mon université, et comme c’était majoritairement rigolo, et que c’est pas forcément un truc qu’on fait souvent, ben en voilà un petit compte-rendu.
Tout a commencé il y a quelques mois : j’ai reçu un mail, je ne sais plus par quel biais (peut-être juste parce que je suis étudiante à l’ETH, peut-être parce que je me suis inscrite dans un coin en disant « ouais, je veux bien participer à ce genre de trucs », je sais plus) qui réclamait des volontaires pour une étude sur l’absorption du fer. Pour la plupart des études de ce genre, je ne peux pas être qualifiée parce que je ne suis pas dans les fourchettes de poids « standard ». Mais là, pour le coup, le poids est précisément le facteur dont ils veulent mesurer l’impact, donc du coup je suis dans la fourchette. Je lis le reste des prérequis, ça a l’air de passer pour tout ; je réponds au mail, on m’envoie le descriptif complet de l’étude, on me demande si ça roule toujours, et on me demande de passer au labo pour un premier entretien. Ledit labo est dans le bâtiment d’à côté du « mien » à l’ETH, donc c’est vraiment pas un problème. L’étude complète « initiale » a quatre rendez-vous après le premier rendez-vous : deux petits déjeuners au labo en conditions « contrôlées », une prise de sang quinze jours plus tard, et un passage à l’université pour une mesure de la composition du corps et une mesure de la fonction musculaire.
Je vais au labo, on me réexplique tout ça, on m’explique que je peux arrêter quand je veux, on me demande si j’ai des questions, tout ça. On m’explique aussi qu’il y a peut-être un test supplémentaire, qu’ils attendent l’accord du comité d’éthique, et ils m’expliquent le test supplémentaire : c’est une mesure de volume sanguin. Je lis, je m’inquiète un peu quand on me dit « le truc c’est qu’on va vous faire respirer une petite quantité de monoxyde de carbone », je suis rassurée quand on m’explique le protocole exact. L’accord du comité d’éthique est arrivé quelques jours plus tard.
Vient le moment de la signature : « j’ai bien compris tout ce qu’on m’a expliqué, je suis d’accord pour participer à l’étude, et j’ai bien noté que je pouvais interrompre ma participation à n’importe quel moment ». Avec, en bonus, une question vraiment difficile : « Si par hasard on trouve une information qui peut avoir un impact sur votre santé, est-ce que vous voulez qu’on vous le dise ou pas ? ». C’est dur, comme question. C’est risquer le faux positif. C’est risquer l’angoisse. Et en même temps, s’il y a quelque chose d’inquiétant, il vaut probablement mieux le savoir, non ? J’ai fini par cocher « oui, dites moi ». Mais non sans hésiter.
Quelques semaines plus tard, j’ai bloqué tous les examens et autres sur deux jours (sauf la prise de sang finale qui devait avoir lieu deux semaines plus tard). Premier rendez-vous, premier petit-déjeuner. Le truc affreux, c’est qu’ils veulent contrôler les paramètres au maximum. Du coup, on m’a demandé de ne rien manger après 20h la veille, et de ne rien boire après minuit la veille. En plein mois de juillet, c’est pas super choupi. Je vais au labo, je mange du pain, du beurre et du miel, un verre d’eau., et une bonne dose d’isotopes de fer, que je n’ai d’ailleurs pas vraiment senti. Je me suis demandé s’ils les avaient mis dans la pâte à pain (parce que le pain était pas terrible :P). Et (sans surprise) on me demande de ne rien manger ni boire pendant 3 heures en suivant. Pareil, mois de juillet, dur. PAS DE CAFÉ, dur.
L’après-midi, je me suis trimbalée à l’autre bout de Zürich pour aller faire le test de volume sanguin. En gros, l’idée c’est de respirer dans divers bidules, plusieurs fois. La première fois dans un spiromètre « à vide » pour regarder la valeur initiale de CO. La deuxième fois dans un gros machin qui leur permet d’injecter une dose contrôlée de CO pendant l’expérience – d’abord un test « à vide » pour expliquer le fonctionnement (il faut expirer le plus possible, tourner un petit robinet, et respirer normalement après – et le tout sans faire rentrer d’air « extérieur » au système), et encore une fois dans le spiromètre pour regarder la valeur « après ». Au passage aussi, quelques prélèvements sanguins dans le lobe de l’oreille, pour mesurer l’hémoglobine et ce genre de trucs. C’était pas super agréable de respirer dans le machin, ou de jouer au spiromètre, parce que c’est globalement pas super confortable d’expirer au maximum. J’en ai profité pour demander comment les isotopes étaient administrés, et en fait ils sont en solution, brossés sur le pain. On m’a demandé si j’avais remarqué le goût, j’ai dit non. J’ai aussi signé une version mise à jour du formulaire de consentement – pour prendre en compte la nouvelle étude. La question « et donc, si on trouve un truc ? » avait gagné un nouveau choix : elle était passée de « oui/non » à « oui/non/décidez pour moi ». J’ai re-coché oui.
Le lendemain matin, deuxième petit déjeuner. Toujours difficile de ne rien boire, et de se passer de café. Il y a deux petits déjeuners parce qu’il y en a un supplémenté en vitamine C : le but du jeu est de voir dans quelle mesure l’ajout de vitamine C aide à l’absorption du fer. Pour ça, ils utilisent deux isotopes différents sur les deux petits-déjeuners. Là par contre, que ce soit parce que c’était moins bien réparti, pas le même isotope, ou parce que j’y faisais plus attention, je suis sortie du labo avec un vilain goût métallique dans la bouche.
L’après-midi, je suis allée à l’université pour aller faire les derniers examens. D’abord, mesure de la composition du corps. C’est pas super rigolo, ça implique essentiellement de pas trop bouger pendant qu’on se fait scanner. Le scanner lui-même balance très peu de radiations (ils disaient l’équivalent de passer trois heures dehors). Je dois dire que j’ai pas été super fan de me voir « complète » sur l’écran, ça fait un drôle d’effet (et la vague impression de prendre beaucoup de place :P). Et pour finir, opération « mesure du fonctionnement musculaire ». Là, l’idée, c’est de sauter de plusieurs manières différentes sur une plaque reliée à un ordinateur. Évidemment, le type qui fait la démo est plutôt du genre sportif (FORCÉMENT, S’IL FAIT QUINZE DÉMOS PAR JOUR, ÇA AIDE), et, bon, faut pas avoir honte 😛 On commence le test, tout se passe bien. Et là, on arrive au moment où il faut sauter à cloche-pied sur la plateforme. Première mesure jambe gauche, OK. (Plutôt mieux que dans l’essai avant, où je m’étais rendue ridicule et où j’avais failli me vautrer). Première mesure jambe droite, OK. Deuxième mesure jambe gauche, OK. Deuxième mesure jambe droite… OK… jusqu’au moment où ma cheville a fait un vilain « clac » et un vilain « aïe » 😦 Je m’étais collé une entorse en janvier, et j’avais pas spécialement réfléchi que c’était peut-être pas l’idée du siècle de sauter dessus comme ça 😦 On me file de la glace, je me traîne difficilement jusqu’au tram en râlant, je rentre à la maison.
J’envoie un mail aux responsables de l’étude pour demander exactement quoi faire niveau assurance, on me répond rapidement, le lendemain béquilles, toubib (parce que je pouvais plus marcher). Bref, je gère tout ça, je tiens les responsables de l’étude au courant, je demande si je qualifie toujours vu qu’on m’a filé des anti-inflammatoires et de l’héparine, on me dit « c’est probablement pas optimal, mais ouais, si tu peux quand même revenir pour la dernière prise de sang, ça serait cool ». Je suppose qu’ils préfèrent avoir les données quitte à exclure après plutôt que de ne pas les avoir du tout.
Mercredi, j’ai été faire la dernière prise de sang (en marchant sur mes deux pieds, ça va mieux 🙂 ). Je sais pas si j’ai déjà vu quelqu’un me faire une prise de sang aussi rapidement, d’ailleurs, c’était impressionnant. Pour me remercier de mon temps et de ma participation, j’ai gagné 150CHF, comme prévu initialement. Je devrais avoir mes propres résultats et les résultats de l’étude quand ils seront prêts.
Bref, globalement, c’était plutôt rigolo, comme expérience. Ça m’a permis de voir comment ce genre d’étude se déroulait, comment ils géraient les expériences et les sujets, tout ça. J’ai trouvé ça cool. Ma cheville moins, mais, bon, comparé à ce que le disciple de Léonard prend dans la gueule, je m’en tire plutôt à bon compte, sur le « je sers la science et c’est ma joie »…
Le blog de Balise 